Page 281 - 8_Snf Tane Tane Matematik

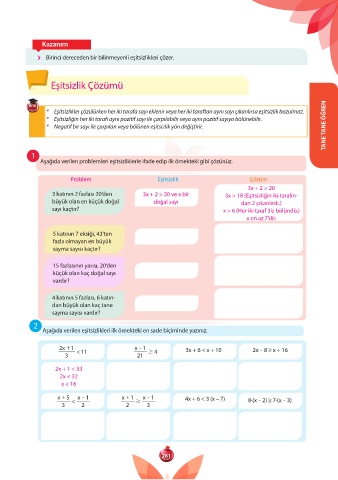
Kazanım

 Birinci dereceden bir bilinmeyenli eşitsizlikleri çözer.

Eşitsizlik Çözümü

* Eşitsizlikler çözülürken her iki tarafa sayı eklenir veya her iki taraftan aynı sayı çıkarılırsa eşitsizlik bozulmaz.
* Eşitsizliğin her iki tarafı aynı pozitif sayı ile çarpılabilir veya aynı pozitif sayıya bölünebilir.
* Negatif bir sayı ile çarpılan veya bölünen eşitsizlik yön değiştirir. TANE TANE ÖĞREN

1
Aşağıda verilen problemleri eşitsizliklerle ifade edip ilk örnekteki gibi çözünüz.

Problem Eşitsizlik Çözüm
3x + 2 > 20
3 katının 2 fazlası 20’den 3x + 2 > 20 ve x bir 3x > 18 (Eşitsizliğin iki tarafın-
büyük olan en küçük doğal doğal sayı dan 2 çıkarılırdı.)
sayı kaçtır? x > 6 (Her iki taraf 3’e bölündü.)
x en az 7’dir.

5 katının 7 eksiği, 43’ten
fazla olmayan en büyük
sayma sayısı kaçtır?

15 fazlasının yarısı, 20’den
küçük olan kaç doğal sayı
vardır?

4 katının 5 fazlası, 6 katın-
dan büyük olan kaç tane
sayma sayısı vardır?
2
Aşağıda verilen eşitsizlikleri ilk örnekteki en sade biçiminde yazınız.

x 2 + 1 < 11 x 1 $ 4 3x + 6 < x + 10 2x – 8 ≥ x + 16
–
3 21

2x + 1 < 33
2x < 32
x < 16

x + 5 < x 1 x 1 $ x 1 4x + 6 < 3 (x – 7) 8·(x – 2) ≥ 7·(x – 3)
+
–
–
3 2 2 3

281