Page 115 - 8_snf_Kirmizi_super_tekrar_matematik_guncel

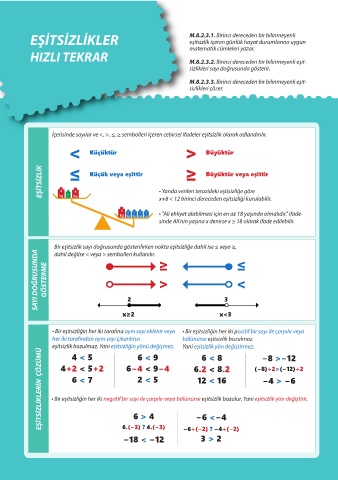
EŞİTSİZLİKLER M.8.2.3.1. Birinci dereceden bir bilinmeyenli
eşitsizlik içeren günlük hayat durumlarına uygun
HIZLI TEKRAR matematik cümleleri yazar.
M.8.2.3.2. Birinci dereceden bir bilinmeyenli eşit-
sizlikleri sayı doğrusunda gösterir.

M.8.2.3.3. Birinci dereceden bir bilinmeyenli eşit-
sizlikleri çözer.

İçerisinde sayılar ve <, >, ≤, ≥ sembolleri içeren cebirsel ifadeler eşitsizlik olarak adlandırılır.
< Küçüktür > Büyüktür

≥
EŞİTSİZLİK kg x ≤ Küçük veya eşittir • Yanda verilen terazideki eşitsizliğe göre
Büyüktür veya eşittir

4
4
kg
4 x+8 < 12 birinci dereceden eşitsizliği kurulabilir.
2 2 2 2 • "Ali ehliyet alabilmesi için en az 18 yaşında olmalıdır." ifade-
kg kg kg kg kg
sinde Ali'nin yaşına x denirse x ≥ 18 olarak ifade edilebilir.

Bir eşitsizlik sayı doğrusunda gösterilirken nokta eşitsizliğe dahil ise ≤ veya ≥,
SAYI DOĞRUSUNDA GÖSTERME ≥ ≤
dahil değilse < veya > sembolleri kullanılır.

<
>

2
3
x≥2 x<3

• Bir eşitsizliğin her iki tarafına aynı sayı eklenir veya • Bir eşitsizliğin her iki pozitif bir sayı ile çarpılır veya
her iki tarafından aynı sayı çıkarılırsa bölünürse eşitsizlik bozulmaz.
eşitsizlik bozulmaz. Yani eşitsizliğin yönü değişmez. Yani eşitsizlik yön değiştirmez. −8 >−12
EŞİTSİZLİKLERİN ÇÖZÜMÜ • Bir eşitsizliğin her iki negatif bir sayı ile çarpılır veya bölünürse eşitsizlik bozulur. Yani eşitsizlik yön değiştirir.
4 < 5
6 < 9
6 < 8
6−4 < 9−4
4+2 < 5+2
6.2 < 8.2
(−8)÷2>(−12)÷2
6 < 7
2 < 5
12 < 16
−4 > −6
6 > 4
−6 <−4
6.(−3) ? 4.(−3)
3 > 2
−18 < −12 −6÷(−2) ? −4÷(−2)