Page 120 - 8_sf_Nar Tanesi Efsane Matematik Deneme

2
Alan πr
D
C
D
C
15 cm
h
Alan = 2πrh
h
A 48 cm 48 cm 2πr 15 cm Alan = 2πrh Alan πr 2
B
A
B
r
2πr
r
Alan πr 2
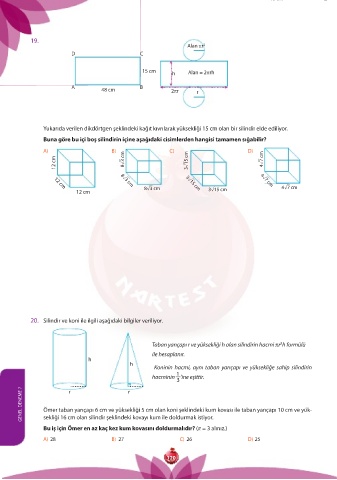
19.
D C Alan πr 2 Alan πr 2
D D C C
15 cm h Alan = 2πrh
15 cm h Alan = 2πrh Alan = 2πrh
15 cm
A B h
A 48 cm B 48 cm 2πr 2πr r
A
48 cm B r 12 cm 2πr 12 cm r 8ñ3 cm 8ñ3 cm
12 cm
12 cm 12 cm 12 cm 8ñ3 cm 8ñ3 cm 8ñ3 cm
8ñ3 cm
Yukarıda verilen dikdörtgen şeklindeki kağıt kıvrılarak yüksekliği 15 cm olan bir silindir elde ediliyor.
Buna göre bu içi boş silindirin içine aşağıdaki cisimlerden hangisi tamamen sığabilir?
A) B) D)
12 cm 12 cm 8ñ3 cm 3ñ15 cm 8ñ3 cm C) 3ñ15 cm 4ñ7 cm 4ñ7 cm
12 cm 8ñ3 cm
12 cm
3ñ15 cm
3ñ15 cm
12 cm 12 cm 8ñ3 cm 8ñ3 cm 8ñ3 cm 3ñ15 cm 3ñ15 cm 4ñ7 cm 4ñ7 cm 4ñ7 cm
4ñ7 cm
12 cm 8ñ3 cm 8ñ3 cm
12 cm
12 cm 8ñ3 cm
3ñ15 cm 3ñ15 cm 3ñ15 cm 4ñ7 cm 4ñ7 cm 4ñ7 cm

3ñ15 cm 4ñ7 cm 4ñ7 cm 4ñ7 cm
3ñ15 cm
3ñ15 cm 4ñ7 cm 4ñ7 cm
3ñ15 cm
3ñ15 cm 4ñ7 cm
3ñ15 cm

20. Silindir ve koni ile ilgili aşağıdaki bilgiler veriliyor.

2
Taban yarıçapı r ve yüksekliği h olan silindirin hacmi πr h formülü
ile hesaplanır.
h
h Koninin hacmi, aynı taban yarıçapı ve yüksekliğe sahip silindirin
1
hacminin 'ine eşittir.
3
GENEL DENEME 7 Ömer taban yarıçapı 6 cm ve yüksekliği 5 cm olan koni şeklindeki kum kovası ile taban yarıçapı 10 cm ve yük-
r
r

sekliği 16 cm olan silindir şeklindeki kovayı kum ile doldurmak istiyor.
Bu iş için Ömer en az kaç kez kum kovasını doldurmalıdır? ( = 3 alınız.)
A) 28 B) 27 C) 26 D) 25

120