Page 92 - 8_sf_Nar Tanesi Efsane Matematik Deneme

İstenilen olası durumların sayısı
11. Bir olayın olma olasılığı=
Tüm olası durumların sayısı

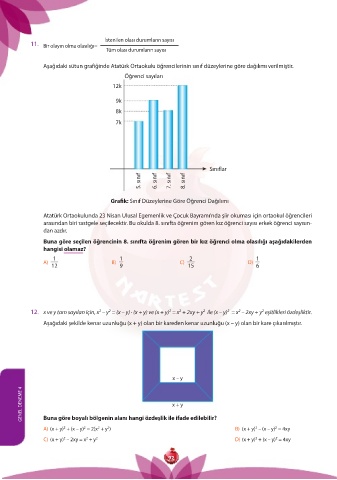
Aşağıdaki sütun grafiğinde Atatürk Ortaokulu öğrencilerinin sınıf düzeylerine göre dağılımı verilmiştir.
Öğrenci sayıları
12k

9k
8k

7k

Sını ar
5. sınıf 6. sınıf 7. sınıf 8. sınıf

Gra k: Sınıf Düzeylerine Göre Öğrenci Dağılımı

Atatürk Ortaokulunda 23 Nisan Ulusal Egemenlik ve Çocuk Bayramı’nda şiir okuması için ortaokul öğrencileri
arasından biri rastgele seçilecektir. Bu okulda 8. sınıfta öğrenim gören kız öğrenci sayısı erkek öğrenci sayısın-
dan azdır.
Buna göre seçilen öğrencinin 8. sınıfta öğrenim gören bir kız öğrenci olma olasılığı aşağıdakilerden
hangisi olamaz?
1 1 2 1
A) B) C) D)
12 9 15 6

2
2
2
12. x ve y tam sayıları için, x – y = (x – y) · (x + y) ve (x + y) = x + 2xy + y ile (x – y) = x – 2xy + y eşitlikleri özdeşliktir.
2
2
2
2
2
Aşağıdaki şekilde kenar uzunluğu (x + y) olan bir kareden kenar uzunluğu (x – y) olan bir kare çıkarılmıştır.

x – y
GENEL DENEME 4 x + y

Buna göre boyalı bölgenin alanı hangi özdeşlik ile ifade edilebilir?
2
2
A) (x + y) + (x – y) = 2(x + y ) B) (x + y) – (x – y) = 4xy
2
2
2
2
2
2
2
2
2
C) (x + y) – 2xy = x + y D) (x + y) + (x – y) = 4xy
92