Page 97 - 8_sf_Power_Up_Den

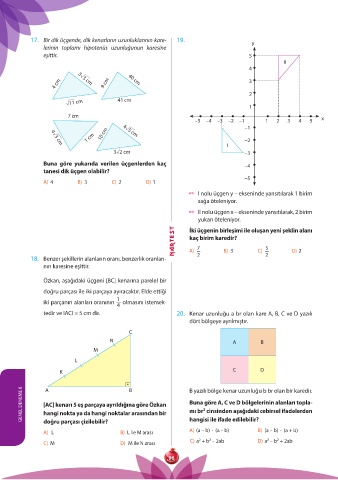
17. Bir dik üçgende, dik kenarların uzunluklarının kare- 19. y
lerinin toplamı hipotenüs uzunluğunun karesine
eşittir. 5
7 cm II
4
4 cm 3ò3 cm 9 cm 40 cm 4ò3 cm 1 cm 10 cm 4ò5 cm 3

2
ò11 cm 41 cm 3ò2 cm
1
7 cm x
–5 –4 –3 –2 –1 –1 1 2 3 4 5

4 cm 3ò3 cm 9 cm 40 cm 4ò3 cm 1 cm 10 cm 4ò5 cm –2
I
ò11 cm 41 cm 3ò2 cm –3
Buna göre yukarıda verilen üçgenlerden kaç –4
tanesi dik üçgen olabilir?
–5
A) 4 B) 3 C) 2 D) 1
✏ I nolu üçgen y – ekseninde yansıtılarak 1 birim
sağa öteleniyor.
✏ II nolu üçgen x – ekseninde yansıtılarak, 2 birim
yukarı öteleniyor.
İki üçgenin birleşimi ile oluşan yeni şeklin alanı
kaç birim karedir?

7
A) B) 3 C) 5 D) 2
18. Benzer şekillerin alanların oranı, benzerlik oranları- 2 2
nın karesine eşittir.

Özkan, aşağıdaki üçgeni [BC] kenarına parelel bir

doğru parçası ile iki parçaya ayıracaktır. Elde ettiği
1
iki parçanın alanları oranının olmasını istemek-
4
tedir ve IACI = 5 cm dir. 20. Kenar uzunluğu a br olan kare A, B, C ve D yazılı
dört bölgeye ayrılmıştır.
C
N A B
M
L
K C D

GENEL DENEME 6 [AC] kenarı 5 eş parçaya ayrıldığına göre Özkan B yazılı bölge kenar uzunluğu b br olan bir karedir.
A
B
Buna göre A, C ve D bölgelerinin alanları topla-
2
mı br cinsinden aşağıdaki cebirsel ifadelerden
hangi nokta ya da hangi noktalar arasından bir
doğru parçası çizilebilir?
A) (a – b) · (a – b)
A) L B) L ile M arası hangisi ile ifade edilebilir? B) (a – b) · (a + b)
2
2
2
2
C) M D) M ile N arası C) a + b – 2ab D) a – b + 2ab
96