Page 40 - 8_sf_Nar Tanesi Efsane Matematik Deneme

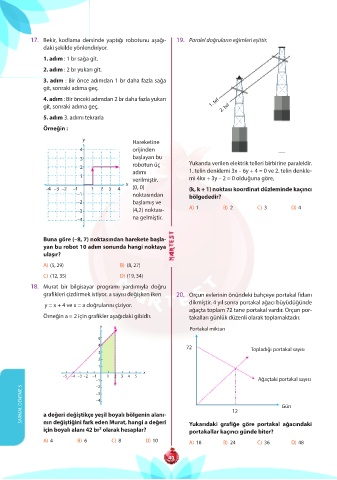
17. Bekir, kodlama dersinde yaptığı robotunu aşağı- 19. Paralel doğruların eğimleri eşittir.
daki şekilde yönlendiriyor.
1. adım : 1 br sağa git.

2. adım : 2 br yukarı git.
3. adım : Bir önce adımdan 1 br daha fazla sağa
git, sonraki adıma geç.
4. adım : Bir önceki adımdan 2 br daha fazla yukarı 1. tel
git, sonraki adıma geç. 2. tel

5. adım 3. adımı tekrarla
Örneğin :
y
Hareketine
4 orijinden
3 başlayan bu Yukarıda verilen elektrik telleri birbirine paraleldir.
2 robotun üç
adımı 1. telin denklemi 3x – 6y + 4 = 0 ve 2. telin denkle-
1 verilmiştir. mi 4kx + 3y – 2 = 0 olduğuna göre,
x
–4 –3 –2 –1 1 2 3 4 (0, 0) (k, k + 1) noktası koordinat düzleminde kaçıncı
–1 noktasından bölgededir?
–2 başlamış ve
–3 (4,2) noktası- A) 1 B) 2 C) 3 D) 4
–4 na gelmiştir.

Buna göre (–8, 7) noktasından harekete başla-
yan bu robot 10 adım sonunda hangi noktaya
ulaşır?
A) (5, 29) B) (8, 27)
C) (12, 35) D) (19, 34)

18. Murat bir bilgisayar programı yardımıyla doğru
grafikleri çizdirmek istiyor. a sayısı değişken iken 20. Orçun evlerinin önündeki bahçeye portakal fidanı
y = x + 4 ve x = a doğrularını çiziyor. dikmiştir. 4 yıl sonra portakal ağacı büyüdüğünde
ağaçta toplam 72 tane portakal vardır. Orçun por-
Örneğin a = 2 için grafikler aşağıdaki gibidir. takalları günlük düzenli olarak toplamaktadır.
y Portakal miktarı

5
4 72 Topladığı portakal sayısı
3
2
1
x
–5 –4 –3 –2 –1 1 2 3 4 5 Ağaçtaki portakal sayısı
–1
–2
SARMAL DENEME 5 a değeri değiştikçe yeşil boyalı bölgenin alanı- 12 Gün
–3
–4

nın değiştiğini fark eden Murat, hangi a değeri
2
için boyalı alanı 42 br olarak hesaplar? Yukarıdaki grafiğe göre portakal ağacındaki
portakallar kaçıncı günde biter?
A) 4 B) 6 C) 8 D) 10 A) 18 B) 24 C) 36 D) 48

40