Page 223 - 7meta_mat

Eşkenar Dörtgen ve Yamuğun Alanı

Çokgenler Öğreten Sorular

Altın Bilgiler
Eşkenar dörtgenin alanı, köşegen uzunluklarının çarpımının yarısına eşittir. Bir yamuğun alanı, taban uzunluklarının toplamı ile,
yüksekliğinin çarpımının yarısına eşittir.
Örnek Örnek

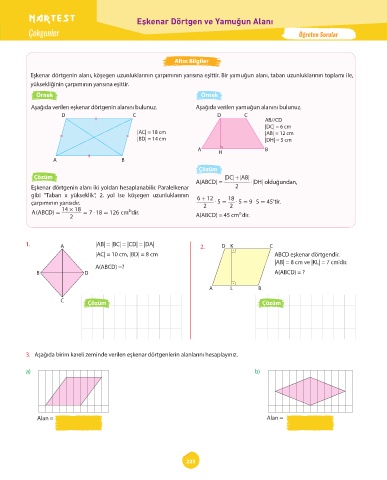
Aşağıda verilen eşkenar dörtgenin alanını bulunuz. Aşağıda verilen yamuğun alanını bulunuz.
D C D C
AB//CD
|DC| = 6 cm
|AC| = 18 cm |AB| = 12 cm
|BD| = 14 cm |DH| = 5 cm
A B
H
A B
Çözüm
Çözüm DC + AB
A(ABCD) = $ DH olduğundan,
Eşkenar dörtgenin alanı iki yoldan hesaplanabilir. Paralelkenar 2
gibi "Taban x yükseklik", 2. yol ise köşegen uzunluklarının 12 18
$
çarpımının yarısıdır. 6 + 2 5 $ = 2 5 $ = 9 5 = 45'tir.
)
$
( AABCD = 14 # 18 = 718 = 126 cm²'dir.
2 A(ABCD) = 45 cm²'dir.

1. A |AB| = |BC| = |CD| = |DA| 2. D K C
|AC| = 10 cm, |BD| = 8 cm ABCD eşkenar dörtgendir.
|AB| = 8 cm ve |KL| = 7 cm'dir.
A(ABCD) =?
B D A(ABCD) = ?

A L B
C Çözüm Çözüm

3. Aşağıda birim kareli zeminde verilen eşkenar dörtgenlerin alanlarını hesaplayınız.

a) b)

Alan = Alan =

223