Page 211 - 8_Snf Tane Tane Matematik

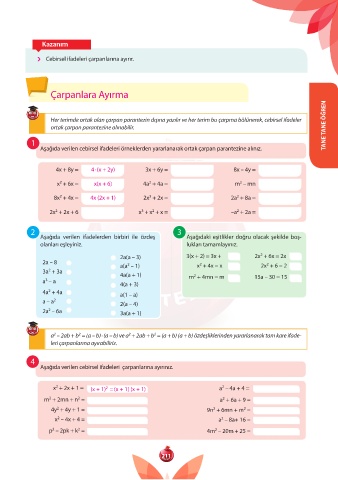
Kazanım

 Cebirsel ifadeleri çarpanlarına ayırır.

Çarpanlara Ayırma

Her terimde ortak olan çarpan parantezin dışına yazılır ve her terim bu çarpma bölünerek, cebirsel ifadeler
ortak çarpan parantezine alınabilir. TANE TANE ÖĞREN
1
Aşağıda verilen cebirsel ifadeleri örneklerden yararlanarak ortak çarpan parantezine alınız.

4x + 8y = 4 · (x + 2y) 3x + 6y = 8x – 4y =

2
x + 6x = x(x + 6) 4a + 4a = m – mn
2
2
2
8x + 4x = 4x (2x + 1) 2x + 2x = 2a + 8a =
2
3
2
3
2
2
2x + 2x + 6 x + x + x = –a + 2a =
2 3
Aşağıda verilen ifadelerden birbiri ile özdeş Aşağıdaki eşitlikler doğru olacak şekilde boş-
olanları eşleyiniz. lukları tamamlayınız.
2
2a(a – 3) 3(x + 2) = 3x + 2x + 6x = 2x
2a – 8
2
2
2
a(a – 1) x + 4x = x 2x + 6 = 2
2
3a + 3a
4a(a + 1) m + 4mn = m 15a – 30 = 15
2
3
a – a 4(a + 3)
2 2
4a + 4a
4a + 4a a(1 – a)
a(1 – a)
a – a
2 2
a – a 2(a – 4)
2(a – 4)
8a + 12 3a(a + 1)
2a – 6a
2
3a(a + 1)
2
2
2
2
a – 2ab + b = (a – b) · (a – b) ve a + 2ab + b = (a + b) (a + b) özdeşliklerinden yararlanarak tam kare ifade-
leri çarpanlarına ayırabiliriz.
4
Aşağıda verilen cebirsel ifadeleri çarpanlarına ayırınız.
x + 2x + 1 = (x + 1) = (x + 1) (x + 1) a – 4a + 4 =
2
2
2
m + 2mn + n = a + 6a + 9 =
2
2
2
2
4y + 4y + 1 = 9n + 6mn + m =
2
2
2
x – 4x + 4 = a – 8a+ 16 =
2
2
2
2
p – 2pk + k = 4m – 20m + 25 =
211