Page 315 - 8_Snf Tane Tane Matematik

Kazanım

 Pisagor bağıntısı oluşturur ilgili problemleri çözer.

Pisagor Bağıntısı

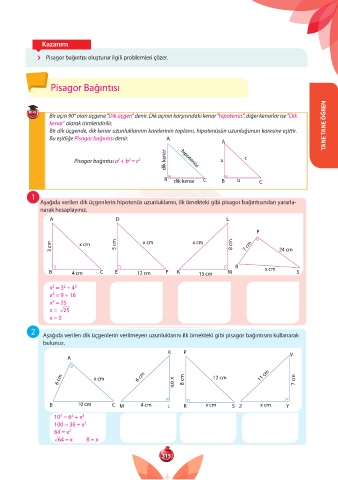
Bir açısı 90° olan üçgene "Dik üçgen" denir. Dik açının karşısındaki kenar "hipotenüs", diğer kenarlar ise "Dik
kenar" olarak isimlendirilir. TANE TANE ÖĞREN
Bir dik üçgende, dik kenar uzunluklarının karelerinin toplamı, hipotenüsün uzunluğunun karesine eşittir.
Bu eşitliğe Pisagor bağıntısı denir. A
A

Pisagor bağıntısı a + b = c d k kenar h potenüs a c
2
2
2
B d k kenar C B b C

1
Aşağıda verilen dik üçgenlerin hipotenüs uzunluklarını, ilk örnekteki gibi pisagor bağıntısından yararla-
narak hesaplayınız.
A D L
P

3 cm x cm 5 cm x cm x cm 8 cm 7 cm 24 cm

R
B 4 cm C E 12 cm F K 15 cm M x cm S

2
2
x = 3 + 4
2
2
x = 9 + 16
2
x = 25
x = ò25
x = 5
2 Aşağıda verilen dik üçgenlerin verilmeyen uzunluklarını ilk örnekteki gibi pisagor bağıntısını kullanarak
bulunuz.
K P
A V

6 cm x cm 6 cm x cm 8 cm 12 cm 11 cm 7 cm

B 10 cm C M 4 cm L R x cm S Z x cm Y

10 = 6 + x
2
2
2
2
100 = 36 + x
64 = x
2
ò64 = x 8 = x
315