Page 239 - 7meta_mat

Çemberin Çevresi

Çember ve Daire Öğreten Sorular

Altın Bilgiler
Yarıçapı r olan çemberin çevresi 2.π.r formülü ile hesaplanır. π sayısı (yaklaşık) 3,14 , 22/7 ya da 3 alınarak daha kolay hesaplamalar
yapılabilir. Çemberin tamamı 360°'lik yay olarak düşünüldüğünde, çemberin bir parçasının (yayın) uzunluğu hesaplanırken orantı
kullanılabilir. Ya da çevre uzunluğu 360°'ye bölünüp, istenen yayı gören merkez açının ölçüsü ile çarpılabilir.

Örnek Örnek
C
O merkezl da re d l m nden

r |OA| = 5 cm olduğuna B |AùBC|’nu bulalım.
O A göre çember n çevres n
bulalım
45°
O 8 cm A

Çözüm Çözüm
π = 3 alalım. 2 · π · r = 2 · 3 · 5 = 30 olduğundan çemberin çevresi
30 cm'dir. π = 3 alalım.
2 $ r r $ $ 45 = 23 8$$ 1 = 6 olduğundan |AùBC| = 6 cm'dir.
$
360 8

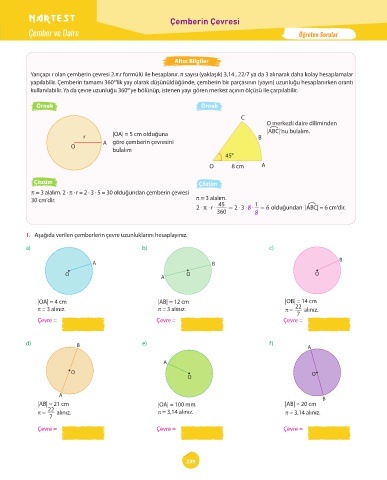
1. Aşağıda verilen çemberlerin çevre uzunluklarını hesaplayınız.

a) b) c)
B
A B
O A O O

|OA| = 4 cm |AB| = 12 cm |OB| = 14 cm
π = 3 alınız. π = 3 alınız. π = 22 alınız.
7
Çevre = Çevre = Çevre =

d) B e) f) A

A
O O
O

A B
|AB| = 21 cm |OA| = 100 mm |AB| = 20 cm
π = 22 alınız. π = 3,14 alınız. π = 3,14 alınız.
7
Çevre = Çevre = Çevre =

239