Page 399 - 100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ-MATEMATİK OLİMPİYATLARI

100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ

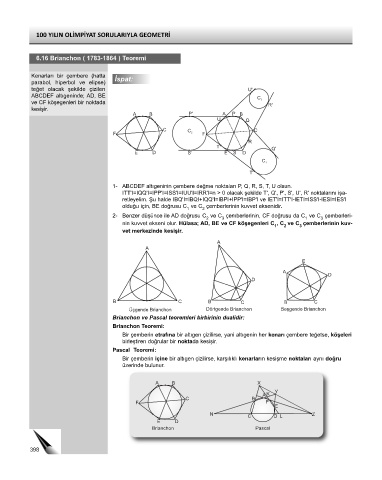
6.16 Brianchon ( 1783-1864 ) Teoremi

Kenarları bir çembere (hatta İspat:
parabol, hiperbol ve elipse)
teğet olacak şekilde çizilen U'
ABCDEF altıgeninde; AD, BE
C 3
ve CF köşegenleri bir noktada R'
kesişir.
A B P' A P B
U Q
C C
F C 2 F
R
T
Q'
E D S' E S D
C 1
T'
1- ABCDEF altıgeninin çembere değme noktaları P, Q, R, S, T, U olsun.
ITT'I=IQQ'I=IPP'I=ISS'I=IUU'I=IRR'I=n > 0 olacak şekilde T', Q', P', S', U', R' noktalarını işa-
retleyelim. Şu halde IBQ'I=IBQI+IQQ'I=IBPI+IPP'I=IBP'I ve IET'I=ITT'I-IETI=ISS'I-IESI=IES'I
olduğu için, BE doğrusu C ve C çemberlerinin kuvvet eksenidir.
1 2
2- Benzer düşünce ile AD doğrusu C ve C çemberlerinin, CF doğrusu da C ve C çemberleri-
2 3 1 3
nin kuvvet ekseni olur. Hülasa; AD, BE ve CF köşegenleri C , C ve C çemberlerinin kuv-
1 2 3
vet merkezinde kesişir.
A
A
E
A
D
D

B C B C B C
Üçgende Brianchon Dörtgende Brianchon Beşgende Brianchon
Brianchon ve Pascal teoremleri birbirinin dualidir:
Brianchon Teoremi:
Bir çemberin etrafına bir altıgen çizilirse, yani altıgenin her kenarı çembere teğetse, köşeleri
birleştiren doğrular bir noktada kesişir.
Pascal Teoremi:
Bir çemberin içine bir altıgen çizilirse, karşılıklı kenarların kesişme noktaları aynı doğru
üzerinde bulunur.

A B X
Y
A K
C B
F F
E
N Z
C D L
E D
Brianchon Pascal

398