Page 66 - 8_snf_Kirmizi_super_tekrar_matematik_guncel

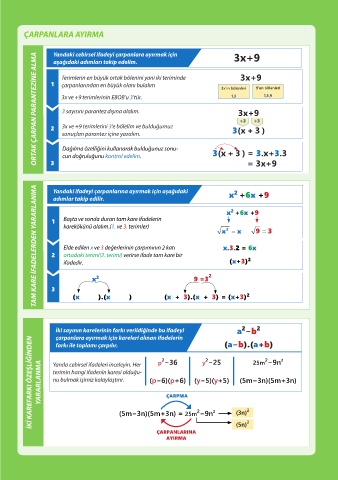
ÇARPANLARA AYIRMA

Yandaki cebirsel ifadeyi çarpanlara ayırmak için 3x+9
ORTAK ÇARPAN PARANTEZİNE ALMA
aşağıdaki adımları takip edelim.

Terimlerin en büyük ortak bölenini yani iki teriminde 3x+9
1 çarpanlarından en büyük olanı bulalım
3x'in bölenleri 9'un bölenleri
3x ve +9 terimlerinin EBOB'u 3'tür. 1,3 1,3,9

3 sayısını parantez dışına alalım. ÇARPMA 3x+9
÷3 ÷3
2 3x ve +9 terimlerini 3'e bölelim ve bulduğumuz 3(x+3 )
sonuçları parantez içine yazalım. 2.(x+4) = 2x+8

Dağılma özelliğini kullanarak bulduğunuz sonu- ÇARPANLARINA
3(x+3 )
cun doğruluğunu kontrol edelim. AYIRMA = 3.x+3.3
3 = 3x+9

TAM KARE İFADELERDEN YARARLANMA
Yandaki ifadeyi çarpanlarına ayırmak için aşağıdaki x +6x +9
2
adımlar takip edilir.
2
x +6x +9
1 Başta ve sonda duran tam kare ifadelerin
karekökünü alalım.(1. ve 3. terimler)
x = x 9 = 3
2
x.3.2 = 6x
Elde edilen x ve 3 değerlerinin çarpımının 2 katı ÇARPMA
2 ortadaki terimi(2. terimi) verirse ifade tam kare bir
ifadedir. (x+3) 2
2.(x+4) = 2x+8
x 2 9 =3 2
3 ÇARPANLARINA
AYIRMA
(x ).(x ) (x + 3).(x + 3) = (x+3) 2

2
2
a −b
İki sayının karelerinin farkı verildiğinde bu ifadeyi (a−b).(a+b)
çarpanlara ayırmak için kareleri alınan ifadelerin
İKİ KAREFARKI ÖZEŞLİĞİNDEN YARARLANMA Yanda cebirsel ifadeleri inceleyin. Her (p−6)(p+6) 2.(x+4) = 2x+8 25m −9n 2
farkı ile toplamı çarpılır.
2
2
2
y −25
p −36
terimin hangi ifadenin karesi olduğu-
nu bulmak işimiz kolaylaştırır.
(y−5)(y+5)
(5m−3n)(5m+3n)
ÇARPMA
ÇARPMA
2
(3n)
(5m−3n)(5m+3n) = 25m −9n
AYIRMA
ÇARPANLARINA 2 ÇARPANLARINA (5n) 2 2
AYIRMA