Page 89 - 100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ-MATEMATİK OLİMPİYATLARI

100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ

Soru:
A A
90°- 2 88° 4°

D D 2°
30° 30°
28° 28°
B C B C
şekil 2
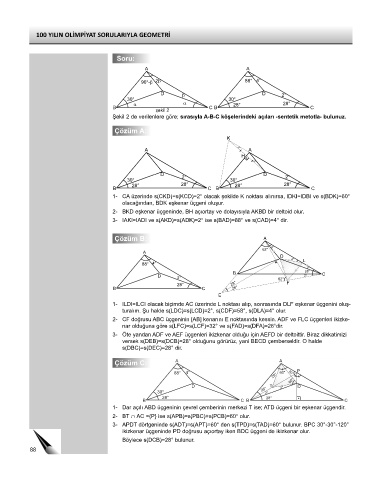
Şekil 2 de verilenlere göre; sırasıyla A-B-C köşelerindeki açıları -sentetik metotla- bulunuz.
Çözüm A:
K
2°
A A
H 2°
D 2° D 2°
30° 30°
28° 28° 28° 28°
B C B C
1- CA üzerinde s(CKD)=s(KCD)=2° olacak şekilde K noktası alınırsa, IDKI=IDBI ve s(BDK)=60°
olacağından, BDK eşkenar üçgeni oluşur.
2- BKD eşkenar üçgeninde, BH açıortay ve dolayısıyla AKBD bir deltoid olur.
3- IAKI=IADI ve s(AKD)=s(ADK)=2° ise s(BAD)=88° ve s(CAD)=4° dir.

Çözüm B: A
4°
62°
A
D
4° L
88° 4°
2°
B 28°
D 2° 62° 2° C
28° 28° F
B C 28°
E
1- ILDI=ILCI olacak biçimde AC üzerinde L noktası alıp, sonrasında DLF eşkenar üçgenini oluş-
turalım. Şu halde s(LDC)=s(LCD)=2°, s(CDF)=58°, s(DLA)=4° olur.
2- CF doğrusu ABC üçgeninin [AB] kenarını E noktasında kessin. ADF ve FLC üçgenleri ikizke-
nar olduğuna göre s(LFC)=s(LCF)=32° ve s(FAD)=s(DFA)=26°dir.
3- Öte yandan ADF ve AEF üçgenleri ikizkenar olduğu için AEFD bir deltoittir. Biraz dikkatimizi
versek s(DEB)=s(DCB)=28° olduğunu görürüz, yani BECD çemberseldir. O halde
s(DBC)=s(DEC)=28° dir.

Çözüm C: A A
28° 60°
88° 4° 60° P
60°
D T 2° D
30° 28° 2°
28° 28°
B C B C
1- Dar açılı ABD üçgeninin çevrel çemberinin merkezi T ise; ATD üçgeni bir eşkenar üçgendir.
2- BT ∩ AC ={P} ise s(APB)=s(PBC)+s(PCB)=60° olur.
3- APDT dörtgeninde s(ADT)=s(APT)=60° den s(TPD)=s(TAD)=60° bulunur. BPC 30°-30°-120°
ikizkenar üçgeninde PD doğrusu açıortay iken BDC üçgeni de ikizkenar olur.
Böylece s(DCB)=28° bulunur.
88