Page 153 - 8pup_mat

TEST Cebirsel İfadeler
38 Özdeşlikleri modellerle açıklar. Cebirsel ifadeleri çarpanlara ayırır.

5. x ve y tam sayıları için, x – y = (x – y) · (x + y) ve (x + y) = x + 2xy + y ile (x – y) = x – 2xy + y eşitlikleri özdeşliktir.
2
2
2
2
2
2
2
2
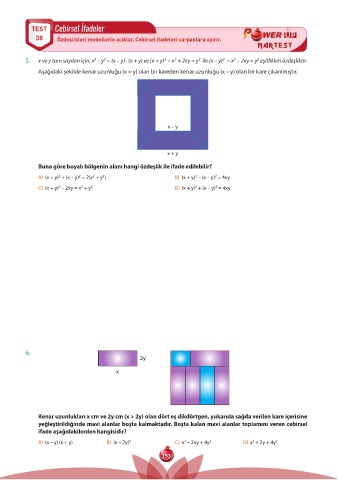
Aşağıdaki şekilde kenar uzunluğu (x + y) olan bir kareden kenar uzunluğu (x – y) olan bir kare çıkarılmıştır.

x – y

x + y

Buna göre boyalı bölgenin alanı hangi özdeşlik ile ifade edilebilir?
2
2
2
2
2
2
A) (x + y) + (x – y) = 2(x + y ) B) (x + y) – (x – y) = 4xy
2
2
2
C) (x + y) – 2xy = x + y D) (x + y) + (x – y) = 4xy
2
2

6.
2y
x

Kenar uzunlukları x cm ve 2y cm (x > 2y) olan dört eş dikdörtgen, yukarıda sağda verilen kare içerisine
yeğleştirildiğinde mavi alanlar boşta kalmaktadır. Boşta kalan mavi alanlar toplamını veren cebirsel
ifade aşağıdakilerden hangisidir?
2
A) (x – y) (x + y) B) (x – 2y) 2 C) x – 2xy + 4y D) x + 2y + 4y 2
2
2
153