Page 95 - 100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ-MATEMATİK OLİMPİYATLARI

100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ

Soru: A A

30° 30°
2°

D D
28°
28°
90°- 88° 4°
2
B C B C
şekil 7
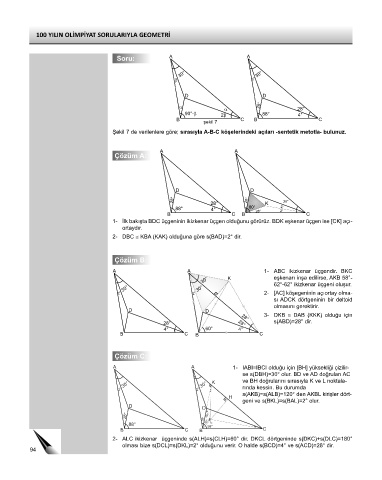
Şekil 7 de verilenlere göre; sırasıyla A-B-C köşelerindeki açıları -sentetik metotla- bulunuz.

Çözüm A:

1- İlk bakışta BDC üçgeninin ikizkenar üçgen olduğunu görürüz. BDK eşkenar üçgen ise [CK] açı-
ortaydır.
2- DBC ≅ KBA (KAK) olduğuna göre s(BAD)=2° dir.

Çözüm B:

A A 1- ABC ikizkenar üçgendir. BKC
30° K eşkenarı inşa edilirse, AKB 58°-
30° 30° 62°-62° ikizkenar üçgeni oluşur.
2° 2° 2- [AC] köşegeninin açıortay olma-
sı ADCK dörtgeninin bir deltoid
olmasını gerektirir.
D D
3- DKB ≅ DAB (KKK) olduğu için
28°
28° 28° s(ABD)=28° dir.
4° 60° 4°
B C B C

Çözüm C:
A A 1- IABI=IBCI olduğu için [BH] yüksekliği çizilir-
se s(DBH)=30° olur. BD ve AD doğruları AC
30° 30° K ve BH doğrularını sırasıyla K ve L noktala-
2° 2° rında kessin. Bu durumda
s(AKB)=s(ALB)=120° den AKBL kirişler dört-
H
geni ve s(BKL)=s(BAL)=2° olur.
D
D
28° 28° 30°
88° 30° 58° L
B C B C
2- ALC ikizkenar üçgeninde s(ALH)=s(CLH)=60° dir. DKCL dörtgeninde s(DKC)+s(DLC)=180°
olması bize s(DCL)=s(DKL)=2° olduğunu verir. O halde s(BCD)=4° ve s(ACD)=28° dir.
94