Page 96 - 100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ-MATEMATİK OLİMPİYATLARI

3. BÖLÜM ÇEMBERLER - I

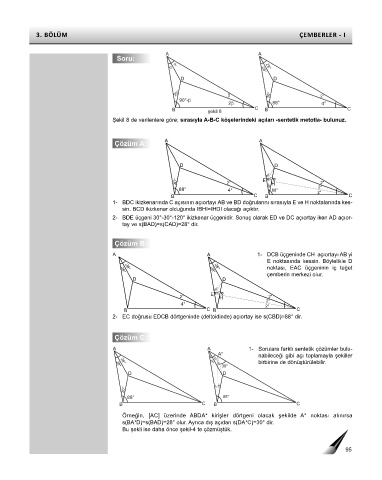
A A
Soru:

28° 28°
D D
30° 30° 2°
90°-
2 88° 4°
B şekil 8 C B C
Şekil 8 de verilenlere göre; sırasıyla A-B-C köşelerindeki açıları -sentetik metotla- bulunuz.

Çözüm A: A A

D D
60°
30° 2° E 60° H 2°
88° 4° 30° 88° 2°
B C B 2° C
1- BDC ikizkenarında C açısının açıortayı AB ve BD doğrularını sırasıyla E ve H noktalarında kes-
sin. BCD ikizkenar olduğunda IBHI=IHDI olacağı açıktır.
2- BDE üçgeni 30°-30°-120° ikizkenar üçgenidir. Sonuç olarak ED ve DC açıortay iken AD açıor-
tay ve s(BAD)=s(CAD)=28° dir.

Çözüm B:

A A 1- DCB üçgeninde CH açıortayı AB yi
E noktasında kessin. Böylelikle D
noktası, EAC üçgeninin iç teğet
28°
28°
28°
28°
çemberin merkezi olur.
D D
60°
E 60°
2° H 2°
2°
4° 2°
B C B C
2- EC doğrusu EDCB dörtgeninde (deltoidinde) açıortay ise s(CBD)=88° dir.
Çözüm C:
A A 1- Sorulara farklı sentetik çözümler bulu-
A* nabileceği gibi açı toplamayla şekiller
birbirine de dönüştürülebilir.
28°
28°
28°
30°
28°
D D
30° 2° 28°
88° 88°
B C B C
Örneğin, [AC] üzerinde ABDA* kirişler dörtgeni olacak şekilde A* noktası alınırsa
s(BA*D)=s(BAD)=28° olur. Ayrıca dış açıdan s(DA*C)=30° dir.
Bu şekli ise daha önce şekil-4 te çözmüştük.

95