Page 373 - 8_sf_Dahimatik

˙
˙
˙
372 DAHIMATIK - Matematik Yarı¸smalarına Ilk Adım M.Özdemir
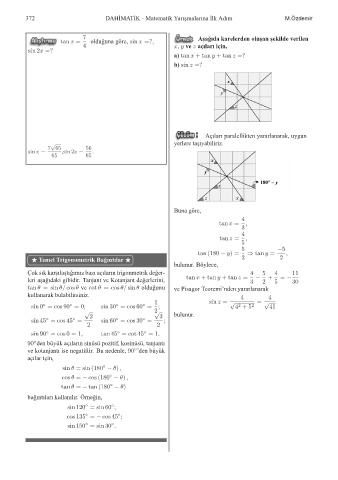
7 A¸sa˘ gıda karelerden olu¸san ¸sekilde verilen
tan x = oldu˘ guna göre, sin x =?;
4 x; y ve z açıları için,
sin 2x =?
a) tan x + tan y + tan z =?
b) sin z =?

Açıları paralellikten yararlanarak, uygun
p yerlere ta¸sıyabiliriz.
7 65 56
sin x = ,sin 2x = .
65 65

Buna göre,
4
tan x = ;
3
4
tan z = ;
5
5 5
tan (180 y) = ) tan y = ;
F Temel Trigonometrik Ba˘ gıntılar F 2 2
bulunur. Böylece,
Çok sık kar¸sıla¸stı˘ gımız bazı açıların trigonmetrik de˘ ger- 4 5 4 11
tan x + tan y + tan z = + =
leri a¸sa˘ gıdaki gibidir. Tanjant ve Kotanjant de˘ gerlerini, 3 2 5 30
tan = sin = cos ve cot = cos = sin oldu˘ gunu ve Pisagor Teoremi’nden yararlanarak
kullanarak bulabilirsiniz. 4 4
1 sin z = p = p
2
sin 0 = cos 90 = 0; sin 30 = cos 60 = ; 4 + 5 2 41

p 2 p
2 3 bulunur.
sin 45 = cos 45 = sin 60 = cos 30 = ;

2 2
sin 90 = cos 0 = 1; tan 45 = cot 45 = 1:

90 den büyük açıların sinüsü pozitif, kosinüsü, tanjantı

ve kotanjantı ise negatiftir. Bu nedenle, 90 ’den büyük
açılar için,
sin = sin (180 ) ;

cos = cos (180 ) ;

tan = tan (180 )

ba˘ gıntıları kullanılır. Örne˘ gin,
sin 120 = sin 60 ;

cos 135 = cos 45 ;

sin 150 = sin 30 :