Page 120 - 100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ-MATEMATİK OLİMPİYATLARI

3. BÖLÜM ÇEMBERLER - I

Soru:
ABC eşkenar üçgeninin [BC] ve [AC] kenarları üzerinde sırasıyla D ve E noktaları;
s(BAD)=15° ve IECI=2IBDI olacak şekilde alınıyor. Buna göre s(EDC) kaç derecedir?

Çözüm:

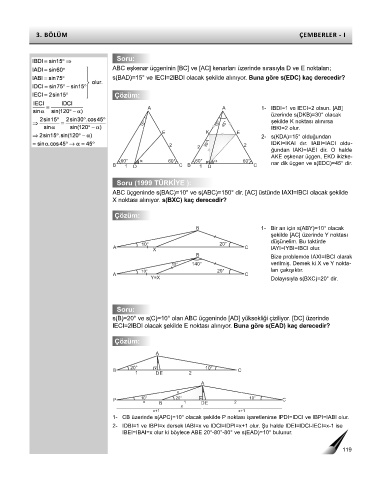
A A 1- IBDI=1 ve IECI=2 olsun. [AB]
üzerinde s(DKB)=30° olacak
15° 15° 45° şekilde K noktası alınırsa
IBKI=2 olur.
E K E
2- s(KDA)=15° olduğundan
2 30° 2 IDKI=IKAI dır. IABI=IACI oldu-
2
ğundan IAKI=IAEI dir. O halde
AKE eşkenar üçgen, EKD ikizke-
60° 60° 60° 60°
B 1 D C B 1 D C nar dik üçgen ve s(EDC)=45° dir.
Soru (1999 TÜRKİYE ):
ABC üçgeninde s(BAC)=10° ve s(ABC)=150° dir. [AC] üstünde IAXI=IBCI olacak şekilde
X noktası alınıyor. s(BXC) kaç derecedir?
Çözüm:

B 1- Bir an için s(ABY)=10° olacak
şekilde [AC] üzerinde Y noktası
düşünelim. Bu taktirde
10° 20°
A C IAYI=IYBI=IBCI olur.
X
B Bize problemde IAXI=IBCI olarak
10° 140° verilmiş. Demek ki X ve Y nokta-
10° 20° ları çakışıktır.
A C
Y=X Dolayısıyla s(BXC)=20° dir.

Soru:
s(B)=20° ve s(C)=10° olan ABC üçgeninde [AD] yüksekliği çiziliyor. [DC] üzerinde
IECI=2IBDI olacak şekilde E noktası alınıyor. Buna göre s(EAD) kaç derecedir?

Çözüm:

A
20° 10°
B C
1 DE 2
A
x
10° 20° 10°
P x B 1 DE 2 C
x
x+1 x+1
1- CB üzerinde s(APC)=10° olacak şekilde P noktası işaretlenirse IPDI=IDCI ve IBPI=IABI olur.
2- IDBI=1 ve IBPI=x dersek IABI=x ve IDCI=IDPI=x+1 olur. Şu halde IDEI=IDCI-IECI=x-1 ise
IBEI=IBAI=x olur ki böylece ABE 20°-80°-80° ve s(EAD)=10° bulunur.

119