Page 117 - 100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ-MATEMATİK OLİMPİYATLARI

100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ

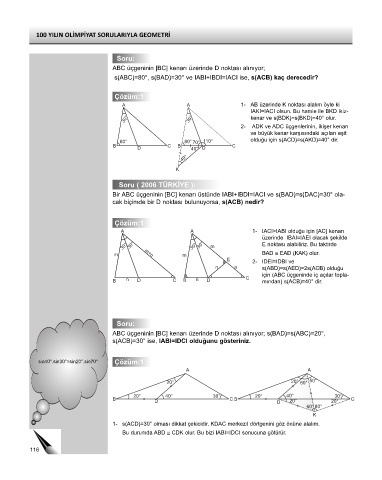
Soru:
ABC üçgeninin [BC] kenarı üzerinde D noktası alınıyor;
s(ABC)=80°, s(BAD)=30° ve IABI+IBDI=IACI ise, s(ACB) kaç derecedir?

Çözüm:1
A A 1- AB üzerinde K noktası alalım öyle ki
IAKI=IACI olsun. Bu hamle ile BKD ikiz-
30° 30° kenar ve s(BDK)=s(BKD)=40° olur.
2- ADK ve ADC üçgenlerinin, ikişer kenarı
ve büyük kenar karşısındaki açıları eşit
80° 80° 70° 110° olduğu için s(ACD)=s(AKD)=40° dir.
B C B C
D 40° D
40°
K

Soru ( 2006 TÜRKİYE ):
Bir ABC üçgeninin [BC] kenarı üstünde IABI+IBDI=IACI ve s(BAD)=s(DAC)=30° ola-
cak biçimde bir D noktası bulunuyorsa, s(ACB) nedir?

Çözüm:1
A A 1- IACI>IABI olduğu için [AC] kenarı
üzerinde IBAI=IAEI olacak şekilde
30° 30° 30° 30° m E noktası alabiliriz. Bu taktirde
m m+n m BAD ≅ EAD (KAK) olur.
E 2- IDEI=IDBI ve
n n s(ABD)=s(AED)=2s(ACB) olduğu
için (ABC üçgeninde iç açılar topla-
B n D C B n D C mından) s(ACB)=40° dir.

Soru:
ABC üçgeninin [BC] kenarı üzerinde D noktası alınıyor; s(BAD)=s(ABC)=20°,
s(ACB)=30° ise, IABI=IDCI olduğunu gösteriniz.

sin40°.sin30°=sin20°.sin70° Çözüm:1
A A

20° 20° 60° 50°
20° 40° 30° 20° 40° 30°
B C B C
D D 20° 20°
60° 80°
K
1- s(ACD)=30° olması dikkat çekicidir. KDAC merkezil dörtgenini göz önüne alalım.
Bu durumda ABD ≅ CDK olur. Bu bizi IABI=IDCI sonucuna götürür.

116