Page 115 - 100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ-MATEMATİK OLİMPİYATLARI

100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ

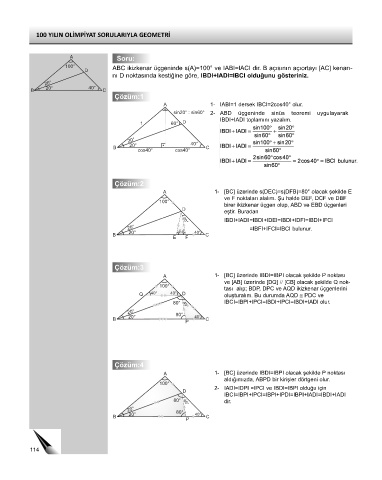
A Soru:
100° ABC ikizkenar üçgeninde s(A)=100° ve IABI=IACI dir. B açısının açıortayı [AC] kenarı-
D
nı D noktasında kestiğine göre, IBDI+IADI=IBCI olduğunu gösteriniz.
20°
20° 40°
B C
Çözüm:1
A 1- IABI=1 dersek IBCI=2cos40° olur.
sin20° : sin60° 2- ABD üçgeninde sinüs teoremi uygulayarak
IBDI+IADI toplamını yazalım.
1 60° D

20°
20° 40°
B C
cos40° cos40°

Çözüm:2
A 1- [BC] üzerinde s(DEC)=s(DFB)=80° olacak şekilde E
ve F noktaları alalım. Şu halde DEF, DCF ve DBF
100°
birer ikizkenar üçgen olup, ABD ve EBD üçgenleri
D
eştir. Buradan
IBDI+IADI=IBDI+IDEI=IBDI+IDFI=IBDI+IFCI
40°
20° =IBFI+IFCI=IBCI bulunur.
20° 80° 80° 40°
B E F C
Çözüm -2

Çözüm:3
A 1- [BC] üzerinde IBDI=IBPI olacak şekilde P noktası
ve [AB] üzerinde [DQ] // [CB] olacak şekilde Q nok-
100°
tası alıp; BDP, DPC ve AQD ikizkenar üçgenlerini
Q 40° 40° D oluşturalım. Bu durumda AQD ≅ PDC ve
80° 40° IBCI=IBPI+IPCI=IBDI+IPCI=IBDI+IADI olur.
20° 80°
20° 40°
B P C
Çözüm -3

Çözüm:4
A 1- [BC] üzerinde IBDI=IBPI olacak şekilde P noktası
aldığımızda, ABPD bir kirişler dörtgeni olur.
100°
2- IADI=IDPI =IPCI ve IBDI=IBPI olduğu için
D
IBCI=IBPI+IPCI=IBPI+IPDI=IBPI+IADI=IBDI+IADI
80° 40° dir.
20° 80°
20° 40°
B P C
Çözüm -4

114