Page 148 - 100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ-MATEMATİK OLİMPİYATLARI

4. BÖLÜM ÜÇGENLER - II

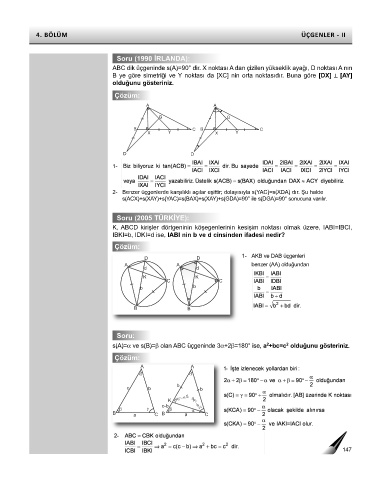
Soru (1990 İRLANDA):
ABC dik üçgeninde s(A)=90° dir. X noktası A dan çizilen yükseklik ayağı, D noktası A nın
B ye göre simetriği ve Y noktası da [XC] nin orta noktasıdır. Buna göre [DX] ⊥ [AY]
olduğunu gösteriniz.
Çözüm:

A A
G G
B C B C
X Y X Y

D D
1-

2- Benzer üçgenlerde karşılıklı açılar eşittir; dolayısıyla s(YAC)=s(XDA) dır. Şu halde
s(ACX)+s(XAY)+s(YAC)=s(BAX)+s(XAY)+s(GDA)=90° ile s(DGA)=90° sonucuna varılır.

Soru (2005 TÜRKİYE):
K, ABCD kirişler dörtgeninin köşegenlerinin kesişim noktası olmak üzere, IABI=IBCI,
IBKI=b, IDKI=d ise, IABI nin b ve d cinsinden ifadesi nedir?
Çözüm:
1- AKB ve DAB üçgenleri
D D
A A benzer (AA) olduğundan
d d
K K
C C
b
b
B B

Soru:
2
2
s(A)=α ve s(B)=β olan ABC üçgeninde 3α+2β=180° ise, a +bc=c olduğunu gösteriniz.
Çözüm:
A A

b
c b b

K
c-b

B B
a C a C

147