Page 151 - 100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ-MATEMATİK OLİMPİYATLARI

100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ

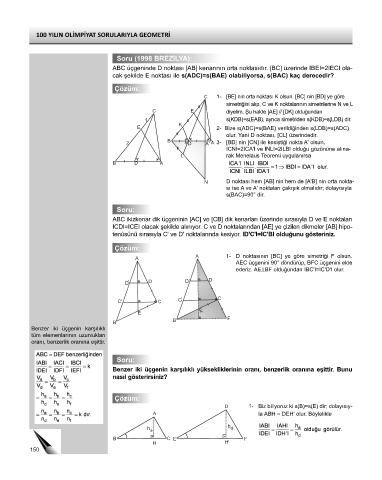
Soru (1998 BREZİLYA):
ABC üçgeninde D noktası [AB] kenarının orta noktasıdır. [BC] üzerinde IBEI=2IECI ola-
cak şekilde E noktası ile s(ADC)=s(BAE) olabiliyorsa, s(BAC) kaç derecedir?
Çözüm:
C 1- [BE] nin orta noktası K olsun. [BC] nin [BD] ye göre
simetriğini alıp, C ve K noktalarının simetrilerine N ve L
C E diyelim. Şu halde [AE] // [DK] olduğundan
1 s(KDB)=s(EAB), ayrıca simetriden s(KDB)=s(LDB) dir.
K
E 2- Bize s(ADC)=s(BAE) verildiğinden s(LDB)=s(ADC)
olur. Yani D noktası, [CL] üzerindedir.
B
2 D A' A 3- [BD] nin [CN] ile kesiştiği nokta A' olsun.
ICNI=2ICA'I ve INLI=2ILBI olduğu gözönüne alına-
L rak Menelaus Teoremi uygulanırsa
B D A

N D noktası hem [AB] nin hem de [A'B] nin orta nokta-
sı ise A ve A' noktaları çakışık olmalıdır; dolayısıyla
s(BAC)=90° dir.
Soru:
ABC ikizkenar dik üçgeninin [AC] ve [CB] dik kenarları üzerinde sırasıyla D ve E noktaları
ICDI=ICEI olacak şekilde alınıyor. C ve D noktalarından [AE] ye çizilen dikmeler [AB] hipo-
tenüsünü sırasıyla C' ve D' noktalarında kesiyor. ID'C'I=IC'BI olduğunu gösteriniz.
Çözüm:
A 1- D noktasının [BC] ye göre simetriği F olsun.
A
AEC üçgenini 90° döndürüp, BFC üçgenini elde
ederiz. AE⊥BF olduğundan IBC'I=IC'D'I olur.
D ' D D' D

C' C C' C
E
E
B F
B
Benzer iki üçgenin karşılıklı
tüm elemenlarının uzunlukları
oranı, benzerlik oranına eşittir.
Soru:
Benzer iki üçgenin karşılıklı yüksekliklerinin oranı, benzerlik oranına eşittir. Bunu
nasıl gösterirsiniz?

Çözüm:
D 1- Biz biliyoruz ki s(B)=s(E) dir; dolayısıy-
A la ABH ≈ DEH' olur. Böylelikle

h a h d
B C E F
H H'
150