Page 249 - 100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ-MATEMATİK OLİMPİYATLARI

100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ

Soru ( 2004 TÜRKİYE ):
Köşeleri, yarıçapı 1 olan çemberin üstünde yer alan düzgün bir n-genin çevre uzunluğu-
nun alanına oranı ise, n kaçtır?

Çözüm:
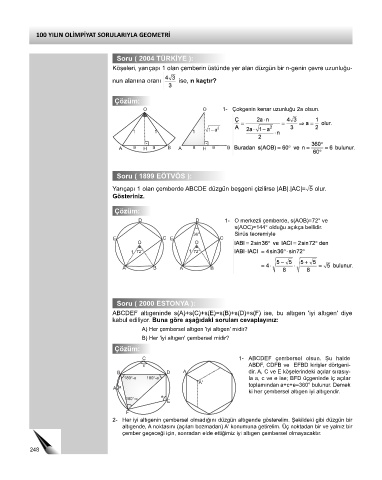
O O 1- Çokgenin kenar uzunluğu 2a olsun.

−
1a 2
1 1 1
A a H a B A a H a B

Soru ( 1899 EÖTVÖS ):

Yarıçapı 1 olan çemberde ABCDE düzgün beşgeni çizilirse |AB|.|AC|=ñ5 olur.
Gösteriniz.

Çözüm:
D D 1- O merkezli çemberde, s(AOB)=72° ve
s(AOC)=144° olduğu açıkça bellidir.
36° Sinüs teoremiyle
E C E C
O O
1 72° 1 72°

A B A B

Soru ( 2000 ESTONYA ):
ABCDEF altıgeninde s(A)+s(C)+s(E)=s(B)+s(D)+s(F) ise, bu altıgen 'iyi altıgen' diye
kabul ediliyor. Buna göre aşağıdaki soruları cevaplayınız:
A) Her çembersel altıgen 'iyi altıgen' midir?
B) Her 'iyi altıgen' çembersel midir?
Çözüm:
C 1- ABCDEF çembersel olsun. Şu halde
c ABDF, CDFB ve EFBD kirişler dörtgeni-
B D A dir. A, C ve E köşelerindeki açılar sırasıy-
°
°
180 -e 180 -a la a, c ve e ise; BFD üçgeninde iç açılar
A'
A a toplamından a+c+e=360° bulunur. Demek
ki her çembersel altıgen iyi altıgendir.
e
180 -c
°
E
F
2- Her iyi altıgenin çembersel olmadığını düzgün altıgende gösterelim. Şekildeki gibi düzgün bir
altıgende, A noktasını (açıları bozmadan) A' konumuna getirelim. Üç noktadan bir ve yalnız bir
çember geçeceği için, sonradan elde ettiğimiz iyi altıgen çembersel olmayacaktır.
248