Page 252 - 100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ-MATEMATİK OLİMPİYATLARI

5. BÖLÜM ÇOKGENLER - II

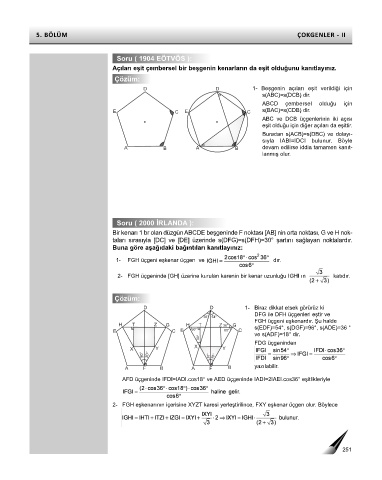
Soru ( 1904 EÖTVÖS ):
Açıları eşit çembersel bir beşgenin kenarların da eşit olduğunu kanıtlayınız.
Çözüm:
D D 1- Beşgenin açıları eşit verildiği için
s(ABC)=s(DCB) dir.
ABCD çembersel olduğu için
E C E C s(BAC)=s(CDB) dir.
ABC ve DCB üçgenlerinin iki açısı
eşit olduğu için diğer açıları da eşittir.
Buradan s(ACB)=s(DBC) ve dolayı-
sıyla IABI=IDCI bulunur. Böyle
A B A B devam edilirse iddia tamamen kanıt-
lanmış olur.

Soru ( 2000 İRLANDA ):
Bir kenarı 1 br olan düzgün ABCDE beşgeninde F noktası [AB] nin orta noktası, G ve H nok-
taları sırasıyla [DC] ve [DE] üzerinde s(DFG)=s(DFH)=30° şartını sağlayan noktalardır.
Buna göre aşağıdaki bağıntıları kanıtlayınız:

1- FGH üçgeni eşkenar üçgen ve dır.

2- FGH üçgeninde [GH] üzerine kurulan karenin bir kenar uzunluğu IGHI ın katıdır.

Çözüm:
D D 1- Biraz dikkat etsek görürüz ki
DFG ile DFH üçgenleri eştir ve
36° 54°
FGH üçgeni eşkenardır. Şu halde
H T Z G H T Z 36° G s(EDF)=54°, s(DGF)=96°, s(ADE)=36 °
E C E 60° 60° C ve s(ADF)=18° dir.
30°
FDG üçgeninden
X
X Y Y
30° 30° 30° 30°
A F B A F B yazılabilir.
AFD üçgeninde IFDI=IADI.cos18° ve AED üçgeninde IADI=2IAEI.cos36° eşitlikleriyle

2- FGH eşkenarının içerisine XYZT karesi yerleştirilince, FXY eşkenar üçgen olur. Böylece

251