Page 265 - 100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ-MATEMATİK OLİMPİYATLARI

100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ

Soru ( 2006 SİNGAPUR ):
ABC üçgeninin dışına; ANC, CLB ve BKA üçgenleri, s(NAC)=s(KBA)=s(LCB) ve
s(NCA)=s(KAB)=s(LBC) olacak şekilde oluşturuluyor. D, E, G ve H noktaları sırasıyla
[AB], [LK], [CA] ve [NA] nın orta noktaları olduğuna göre, DEGH dörtgeni bir paralel-
kenardır, gösteriniz.
Çözüm:
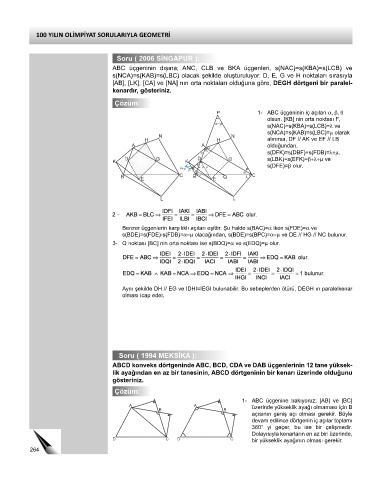
P 1- ABC üçgeninin iç açıları α, β, θ
olsun. [KB] nin orta noktası F,

s(NAC)=s(KBA)=s(LCB)=λ ve
s(NCA)=s(KAB)=s(LBC)=μ olarak
N N
H H alınırsa, DF // AK ve EF // LB
A A olduğundan,

s(DFK)=s(DBF)+s(FDB)=λ+μ,
D G D G s(LBK)=s(EFK)=β+λ+μ ve
K K
s(DFE)=β olur.

F

B C B Q C
E E
L L
Benzer üçgenlerin karşılıklı açıları eşittir. Şu halde s(BAC)=α iken s(FDE)=α ve
s(BDE)=s(FDE)-s(FDB)=α−μ olacağından, s(BDE)=s(BPC)=α−μ ve DE // HG // NC bulunur.
3- Q noktası [BC] nin orta noktası ise s(BDQ)=α ve s(EDQ)=μ olur.

Aynı şekilde DH // EG ve IDHI=IEGI bulunabilir. Bu sebeplerden ötürü, DEGH ın paralelkenar
olması icap eder.

Soru ( 1994 MEKSİKA ):
ABCD konveks dörtgeninde ABC, BCD, CDA ve DAB üçgenlerinin 12 tane yüksek-
lik ayağından en az bir tanesinin, ABCD dörtgeninin bir kenarı üzerinde olduğunu
gösteriniz.
Çözüm:
1- ABC üçgenine bakıyoruz; [AB] ve [BC]
A A üzerinde yükseklik ayağı olmaması için B
B B
açısının geniş açı olması gerekir. Böyle
devam edilince dörtgenin iç açılar toplamı
360° yi geçer, bu ise bir çelişmedir.
Dolayısıyla kenarların en az biri üzerinde,
D C D C bir yükseklik ayağının olması gerekir.
264