Page 271 - 100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ-MATEMATİK OLİMPİYATLARI

100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ

5.3.5 Brahmagupta ( 598-668 ) Teoremi

Köşegenleri dik kesişen kiriş- İspat:
ler dörtgeninde, köşegenlerin
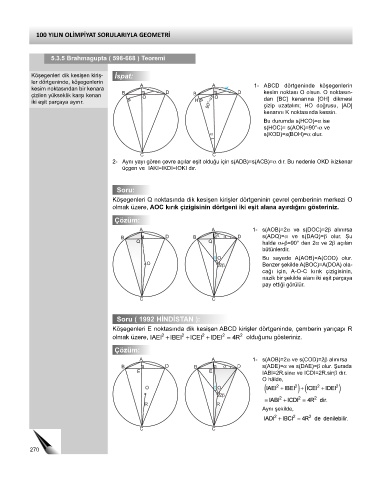
A A 1- ABCD dörtgeninde köşegenlerin
kesim noktasından bir kenara K
B D B D kesim noktası O olsun. O noktasın-
çizilen yükseklik karşı kenarı
O O dan [BC] kenarına [OH] dikmesi
iki eşit parçaya ayırır. H 90°- çizip uzatalım; HO doğrusu, [AD]
kenarını K noktasında kessin.
Bu durumda s(HCO)=α ise
s(HOC)= s(AOK)=90°-α ve
s(KOD)=s(BOH)=α olur.

C C
2- Aynı yayı gören çevre açılar eşit olduğu için s(ADB)=s(ACB)=α dır. Bu nedenle OKD ikizkenar
üçgen ve IAKI=IKDI=IOKI dır.

Soru:
Köşegenleri Q noktasında dik kesişen kirişler dörtgeninin çevrel çemberinin merkezi O
olmak üzere, AOC kırık çizigisinin dörtgeni iki eşit alana ayırdığını gösteriniz.
Çözüm:
A A 1- s(AOB)=2α ve s(DOC)=2β alınırsa
B D B D s(ADQ)=α ve s(DAQ)=β olur. Şu
Q Q halde α+β=90° den 2α ve 2β açıları
bütünlerdir.
O Bu sayede A(AOB)=A(COD) olur.
2
O
2 Benzer şekilde A(BOC)=A(DOA) ola-
cağı için, A-O-C kırık çizigisinin,
nazik bir şekilde alanı iki eşit parçaya
pay ettiği görülür.
C C

Soru ( 1992 HİNDİSTAN ):
Köşegenleri E noktasında dik kesişen ABCD kirişler dörtgeninde, çemberin yarıçapı R
olmak üzere, olduğunu gösteriniz.

Çözüm:
A A 1- s(AOB)=2α ve s(COD)=2β alınırsa
B D B D s(ADE)=α ve s(DAE)=β olur. Şurada
E E IABI=2R.sinα ve ICDI=2R.sinβ dır.
O hâlde,
O 2 O
2
R R
Aynı şekilde,

C C

270