Page 272 - 100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ-MATEMATİK OLİMPİYATLARI

ÇOKGENLER - II

Soru:
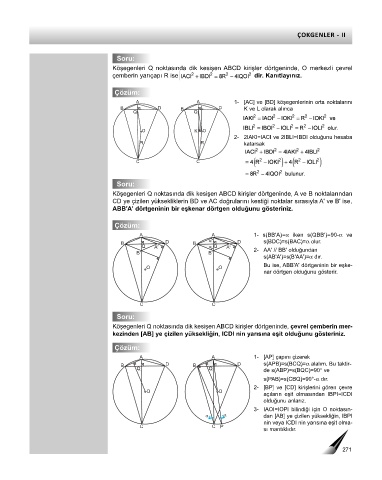
Köşegenleri Q noktasında dik kesişen ABCD kirişler dörtgeninde, O merkezli çevrel
çemberin yarıçapı R ise dir. Kanıtlayınız.

Çözüm:
A A 1- [AC] ve [BD] köşegenlerinin orta noktalarını
B D B L D K ve L olarak alınca
Q Q

O K O
2- 2IAKI=IACI ve 2IBLI=IBDI olduğunu hesaba
R R katarsak

C C

Soru:
Köşegenleri Q noktasında dik kesişen ABCD kirişler dörtgeninde, A ve B noktalarından
CD ye çizilen yüksekliklerin BD ve AC doğrularını kestiği noktalar sırasıyla A' ve B' ise,
ABB'A' dörtgeninin bir eşkenar dörtgen olduğunu gösteriniz.

Çözüm:
A A 1- s(BB'A)=α iken s(QBB')=90-α ve
B D B D s(BDC)=s(BAC)=α olur.
Q A' Q A'
B' B' 2- AA' // BB' olduğundan
s(AB'A')=s(B'AA')=α dır.
Bu ise, ABB'A' dörtgeninin bir eşke-
O O
nar dörtgen olduğunu gösterir.

C C
Soru:
Köşegenleri Q noktasında dik kesişen ABCD kirişler dörtgeninde, çevrel çemberin mer-
kezinden [AB] ye çizilen yüksekliğin, ICDI nin yarısına eşit olduğunu gösteriniz.
Çözüm:
A A 1- [AP] çapını çizerek
B D B D s(APB)=s(BCQ)=α alalım. Bu taktir-
Q Q de s(ABP)=s(BQC)=90° ve
s(PAB)=s(CBQ)=90° -α dır.
2- [BP] ve [CD] kirişlerini gören çevre
O O
açıların eşit olmasından IBPI=ICDI
olduğunu anlarız.
3- IAOI=IOPI bilindiği için O noktasın-
dan [AB] ye çizilen yüksekliğin, IBPI
nin veya ICDI nin yarısına eşit olma-
C C P
sı mantıklıdır.

271