Page 390 - 100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ-MATEMATİK OLİMPİYATLARI

6. BÖLÜM ÇEMBERLER - II

6.10 Euler ( 1707 - 1783 ) Teoremi

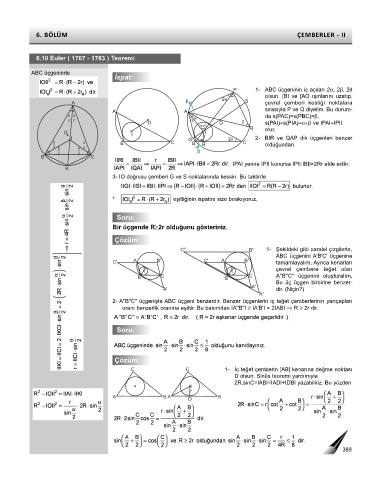
ABC üçgeninde
İspat:
P 1- ABC üçgeninin iç açıları 2α, 2β, 2θ
olsun. [BI ve [AO ışınlarını uzatıp,
2 S
A çevrel çemberi kestiği noktalara
A A sırasıyla P ve Q diyelim. Bu durum-
α α da s(PAC)=s(PBC)=β,
2 2
O O s(PAI)=s(PIA)=α+β ve IPAI=IPII

Q olur.
O I I
I G r 2 2- BIR ve QAP dik üçgenleri benzer
β θ B C B R C
2 β θ 2 olduğundan
2 2
B C
IPAI yerine IPII konursa IPII.IBII=2Rr elde edilir.
K
3- IO doğrusu çemberi G ve S noktalarında kessin. Bu taktirde
* eşitliğinin ispatını size bırakıyoruz.

Soru:
Bir üçgende R≥2r olduğunu gösteriniz.

Çözüm:
C'' B'' 1- Şekildeki gibi paralel çizgilerle,
ABC üçgenini A'B'C' üçgenine
C' A B' C' A B' tamamlayalım. Ayrıca kenarları
r r çevrel çembere teğet olan
I I
B C B C A''B''C'' üçgenini oluşturalım.
Bu üç üçgen birbirine benzer-
A'
A' dir. (Niçin?)
A''
2- A''B''C'' üçgeniyle ABC üçgeni benzerdir. Benzer üçgenlerin iç teğet çemberlerinin yarıçapları
oranı benzerlik oranına eşittir. Bu bakımdan IA''B''I ≥ IA'B'I = 2IABI ⇒ R ≥ 2r dir.

Soru:

Çözüm:
C C 1- İç teğet çemberin [AB] kenarına değme noktası
D olsun. Sinüs teoremi yardımıyla
2R.sinC=IABI=IADI+IDBI yazabiliriz. Bu yüzden
I
r
A B A B
D

389