Page 41 - 100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ-MATEMATİK OLİMPİYATLARI

100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ

Soru:
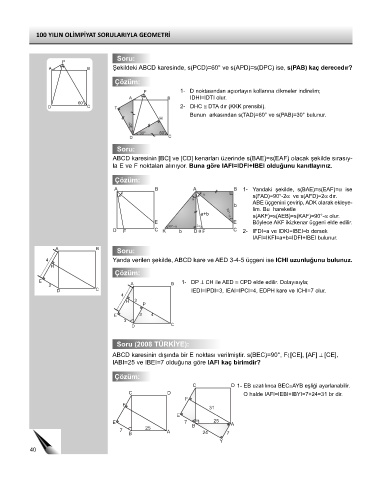
Şekildeki ABCD karesinde, s(PCD)=60° ve s(APD)=s(DPC) ise, s(PAB) kaç derecedır?
Çözüm:
1- D noktasından açıortayın kollarına dikmeler indirelim;
IDHI=IDTI olur.
2- DHC ≅ DTA dır (KKK prensibi).
Bunun arkasından s(TAD)=60° ve s(PAB)=30° bulunur.

Soru:
ABCD karesinin [BC] ve [CD] kenarları üzerinde s(BAE)=s(EAF) olacak şekilde sırasıy-
la E ve F noktaları alınıyor. Buna göre IAFI=IDFI+IBEI olduğunu kanıtlayınız.

Çözüm:
1- Yandaki şekilde, s(BAE)=s(EAF)=α ise
s(FAD)=90°-2α ve s(AFD)=2α dır.
ABE üçgenini çevirip, ADK olarak ekleye-
lim. Bu hareketle
s(AKF)=s(AEB)=s(KAF)=90°-α olur.
Böylece AKF ikizkenar üçgeni elde edilir.
2- IFDI=a ve IDKI=IBEI=b dersek
IAFI=IKFI=a+b=IDFI+IBEI bulunur.

Soru:
A B
4 Yanda verilen şekilde, ABCD kare ve AED 3-4-5 üçgeni ise ICHI uzunluğunu bulunuz.
H
Çözüm:
E 1- DP ⊥ CH ile AED ≅ CPD elde edilir. Dolayısıyla;
3 A B
D C IEDI=IPDI=3, IEAI=IPCI=4, EDPH kare ve ICHI=7 olur.
4
H 3
P
E 3 4
3
D C

Soru (2008 TÜRKİYE):
ABCD karesinin dışında bir E noktası verilmiştir. s(BEC)=90°, F([CE], [AF] ⊥ [CE],
IABI=25 ve IBEI=7 olduğuna göre IAFI kaç birimdir?
Çözüm:
C D 1- EB uzatılınca BEC≅AYB eşliği ayarlanabilir.
C D O halde IAFI=IEBI+IBYI=7+24=31 br dir.
F
F
31
E
E 7 25 A
25 B
7 A
B 24 7
Y
40