Page 59 - 100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ-MATEMATİK OLİMPİYATLARI

100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ

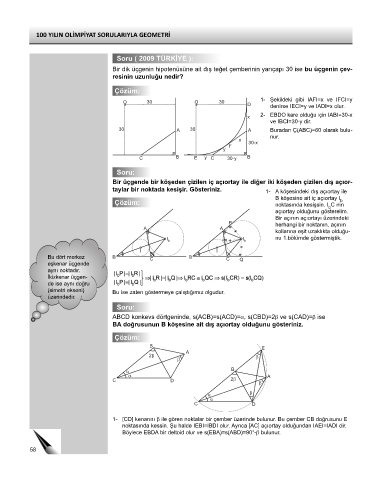
Soru ( 2009 TÜRKİYE ):
Bir dik üçgenin hipotenüsüne ait dış teğet çemberinin yarıçapı 30 ise bu üçgenin çev-
resinin uzunluğu nedir?

Çözüm:
1- Şekildeki gibi IAFI=x ve IFCI=y
O 30 O 30
D denirse IECI=y ve IADI=x olur.
x 2- EBDO kare olduğu için IABI=30-x
ve IBCI=30-y dir.
30 A 30 A Buradan Ç(ABC)=60 olarak bulu-
nur.
x
30-x
F
y
C B E y C 30-y B
Soru:
Bir üçgende bir köşeden çizilen iç açıortay ile diğer iki köşeden çizilen dış açıor-
taylar bir noktada kesişir. Gösteriniz. 1- A köşesindeki dış açıortay ile
B köşesine ait iç açıortay I
Çözüm: noktasında kesişsin. I C nin
b
b
açıortay olduğunu gösterelim.
Bir açının açıortayı üzerindeki
P
herhangi bir noktanın, açının
A A
kollarına eşit uzaklıkta olduğu-
b I R b I nu 1.bölümde göstermiştik.
I I
Bu dört merkez B B
C C Q
eşkenar üçgende
aynı noktadır.
İkizkenar üçgen-
de ise aynı doğru
(simetri ekseni) Bu ise zaten göstermeye çalıştığımız olgudur.
üzerindedir.
Soru:
ABCD konkevs dörtgeninde, s(ACB)=s(ACD)=α, s(CBD)=2β ve s(CAD)=β ise
BA doğrusunun B köşesine ait dış açıortay olduğunu gösteriniz.
Çözüm:
B
E
A
2

B

A
C D 2

C D
1- [CD] kenarını β ile gören noktalar bir çember üzerinde bulunur. Bu çember CB doğrusunu E
noktasında kessin. Şu halde IEBI=IBDI olur. Ayrıca [AC] açıortay olduğundan IAEI=IADI dir.
Böylece EBDA bir deltoid olur ve s(EBA)=s(ABD)=90°-β bulunur.

58