Page 64 - 100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ-MATEMATİK OLİMPİYATLARI

3. BÖLÜM ÇEMBERLER - I

Soru (2001 BALTIK ÜLKELERİ ):
Bir çember üzerinde A, B, C, D, E noktaları AB // EC ve AC // ED olacak şekilde alını-
yor. E noktasından çizilen teğet AB yi P noktasında kesiyor. BD ve EC nin kesişim nok-
tası Q ise, ICAI=IPQI olduğunu gösteriniz.
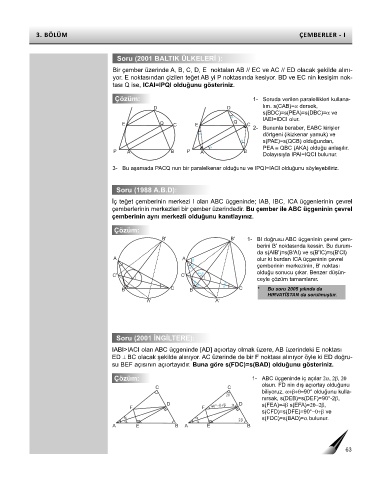
Çözüm: 1- Soruda verilen paralellikleri kullana-
D D lım. s(CAB)=α dersek,
s(BDC)=s(PEA)=s(DBC)=α ve
IAEI=IDCI olur.
E Q C E Q C
2- Bununla beraber, EABC kirişler
dörtgeni (ikizkenar yamuk) ve
s(PAE)=s(QCB) olduğundan,
PEA ≅ QBC (AKA) olduğu anlaşılır.
P A B P A B
Dolayısıyla IPAI=IQCI bulunur.
3- Bu aşamada PACQ nun bir paralelkenar olduğunu ve IPQI=IACI olduğunu söyleyebiliriz.

Soru (1988 A.B.D):
İç teğet çemberinin merkezi I olan ABC üçgeninde; IAB, IBC, ICA üçgenlerinin çevrel
çemberlerinin merkezleri bir çember üzerindedir. Bu çember ile ABC üçgeninin çevrel
çemberinin aynı merkezli olduğunu kanıtlayınız.

Çözüm:
B' B' 1- BI doğrusu ABC üçgeninin çevrel çem-
berini B' noktasında kessin. Bu durum-
da s(AIB')=s(B'AI) ve s(B'IC)=s(B'CI)
A A olur ki burdan ICA üçgeninin çevrel
çemberinin merkezinin, B' noktası

olduğu sonucu çıkar. Benzer düşün-
C' C'
I I ceyle çözüm tamamlanır.

B C B C * Bu soru 2005 yılında da
HIRVATİSTAN da sorulmuştur.
A' A'

Soru (2001 İNGİLTERE):

IABI>IACI olan ABC üçgeninde [AD] açıortay olmak üzere, AB üzerindeki E noktası
ED ⊥ BC olacak şekilde alınıyor. AC üzerinde de bir F noktası alınıyor öyle ki ED doğru-
su BEF açısının açıortayıdır. Buna göre s(FDC)=s(BAD) olduğunu gösteriniz.

Çözüm: 1- ABC üçgeninde iç açılar 2α, 2β, 2θ
olsun. FD nin dış açıortay olduğunu
C C
biliyoruz. α+β+θ=90° olduğunu kulla-

nırsak, s(DEB)=s(DEF)=90°-2β,
D D s(FEA)=4β s(EFA)=2θ−2β,
F F
s(CFD)=s(DFE)=90°−θ+β ve
s(FDC)=s(BAD)=α bulunur.

A E B A E B
63