Page 63 - 100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ-MATEMATİK OLİMPİYATLARI

100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ

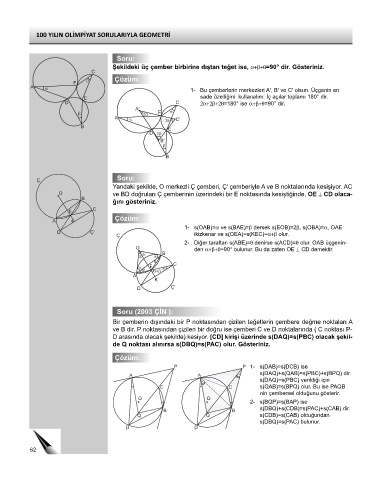
Soru:
Şekildeki üç çember birbirine dıştan teğet ise, α+β+θ=90° dir. Gösteriniz.
C
Çözüm:

F
A 1- Bu çemberlerin merkezleri A', B' ve C' olsun. Üçgenin en
E sade özelliğini kullanalım: İç açılar toplamı 180° dir.
D C 2α+2β+2θ=180° ise α+β+θ=90° dir.
A'
F
A C'
B
E
D
B'

B

Soru:
Ç
Yandaki şekilde, O merkezli Ç çemberi, Ç' çemberiyle A ve B noktalarında kesişiyor. AC
O ve BD doğruları Ç çemberinin üzerindeki bir E noktasında kesiştiğinde, OE ⊥ CD olaca-
B
ğını gösteriniz.
C
E
Çözüm:
A
1- s(OAB)=α ve s(BAE)=β dersek s(EOB)=2β, s(OBA)=α, OAE
D Ç'
Ç ikizkenar ve s(OEA)=s(KEC)=α+β olur.
2- Diğer taraftan s(ABE)=θ denirse s(ACD)=θ olur. OAB üçgenin-
O den α+β+θ=90° bulunur. Bu da zaten OE ⊥ CD demektir.
B

E C

A
K
D Ç’
Soru (2003 ÇİN ):
Bir çemberin dışındaki bir P noktasından çizilen teğetlerin çembere değme noktaları A
ve B dir. P noktasından çizilen bir doğru ise çemberi C ve D noktalarında ( C noktası P-
D arasında olacak şekilde) kesiyor. [CD] kirişi üzerinde s(DAQ)=s(PBC) olacak şekil-
de Q noktası alınırsa s(DBQ)=s(PAC) olur. Gösteriniz.
Çözüm:
P P 1- s(DAB)=s(DCB) ise
s(DAQ)+s(QAB)=s(PBC)+s(BPQ) dir.
A A
s(DAQ)=s(PBC) verildiği için
C C s(QAB)=s(BPQ) olur. Bu ise PAQB
nin çembersel olduğunu gösterir.
O O
2- s(BQP)=s(BAP) ise
s(DBQ)+s(CDB)=s(PAC)+s(CAB) dir.
B B
Q Q s(CDB)=s(CAB) olduğundan
s(DBQ)=s(PAC) bulunur.
D D

62