Page 65 - 100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ-MATEMATİK OLİMPİYATLARI
P. 65
100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ
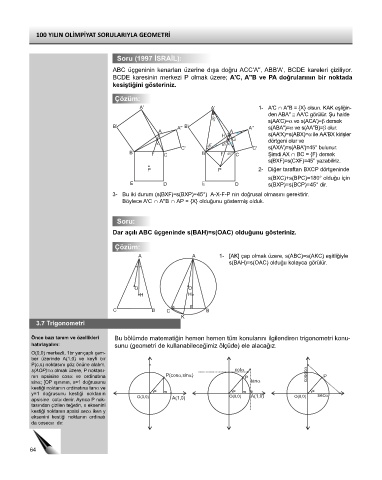
Soru (1997 İSRAİL):
ABC üçgeninin kenarları üzerine dışa doğru ACC'A'', ABB'A', BCDE kareleri çiziliyor.
BCDE karesinin merkezi P olmak üzere; A'C, A''B ve PA doğrularının bir noktada
kesiştiğini gösteriniz.
Çözüm:
A' A' 1- A'C ∩ A''B = {X} olsun. KAK eşliğin-
den ABA'' ≅ AA'C görülür. Şu halde
45° s(AA'C)=α ve s(ACA')=β dersek
B' A'' B' A'' s(ABA'')=α ve s(AA''B)=β olur.
A A
H s(AA'X)=s(ABX)=α ile AA'BX kirişler
G dörtgeni olur ve
X 45° 45° X
C' C' s(AXA')=s(ABA')=45° bulunur.
B F C B F 45° C Şimdi AX ∩ BC = {F} dersek
s(BXF)=s(CXF)=45° yazabiliriz.
P P 2- Diğer taraftan BXCP dörtgeninde
s(BXC)+s(BPC)=180° olduğu için
E D E D s(BXP)=s(BCP)=45° dir.
3- Bu iki durum (s(BXF)=s(BXP)=45°) A-X-F-P nin doğrusal olmasını gerektirir.
Böylece A'C ∩ A''B ∩ AP = {X} olduğunu göstermiş olduk.
Soru:
Dar açılı ABC üçgeninde s(BAH)=s(OAC) olduğunu gösteriniz.
Çözüm:
A A 1- [AK] çap olmak üzere, s(ABC)=s(AKC) eşitliğiyle
s(BAH)=s(OAC) olduğu kolayca görülür.
O O
H H
C B C B
K
3.7 Trigonometri
Önce bazı tanım ve özellikleri Bu bölümde matematiğin hemen hemen tüm konularını ilgilendiren trigonometri konu-
hatırlayalım: sunu (geometri de kullanabileceğimiz ölçüde) ele alacağız.
O(0,0) merkezli, 1br yarıçaplı çem-
ber üzerinde A(1,0) ve keyfi bir
P(c,s) noktasını göz önüne alalım.
s(AOP)=α olmak üzere, P noktası- cot
nın apsisine cosα ve ordinatına P(cos ,sin ) P cosec P
sinα; [OP ışınının, x=1 doğrusunu tan
kestiği noktanın ordinatına tanα ve
y=1 doğrusunu kestiği noktanın
O(0,0) A(1,0) O(0,0) A(1,0) O(0,0) sec
apsisine cotα denir. Ayrıca P nok-
tasından çizilen teğetin, x eksenini
kestiği noktanın apsisi secα iken y
eksenini kestiği noktanın ordinatı
da cosecα dır.
64