Page 103 - 100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ-MATEMATİK OLİMPİYATLARI

100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ

Soru:
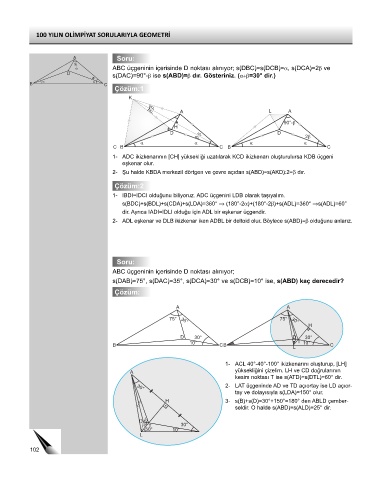
ABC üçgeninin içerisinde D noktası alınıyor; s(DBC)=s(DCB)=α, s(DCA)=2β ve
s(DAC)=90°-β ise s(ABD)=β dır. Gösteriniz. (α+β=30° dir.)
Çözüm:1
K

A L A
90°-
H
D D
2

C B C B C
1- ADC ikizkenarının [CH] yüksekliği uzatılarak KCD ikizkenarı oluşturulursa KDB üçgeni
eşkenar olur.
2- Şu halde KBDA merkezil dörtgen ve çevre açıdan s(ABD)=s(AKD):2=β dır.
Çözüm:2
1- IBDI=IDCI olduğunu biliyoruz. ADC üçgenini LDB olarak taşıyalım.
s(BDC)+s(BDL)+s(CDA)+s(LDA)=360° ⇒ (180°-2α)+(180°-2β)+s(ADL)=360° ⇒s(ADL)=60°
dir. Ayrıca IADI=IDLI olduğu için ADL bir eşkenar üçgendir.
2- ADL eşkenar ve DLB ikizkenar iken ADBL bir deltoid olur. Böylece s(ABD)=β olduğunu anlarız.

Soru:
ABC üçgeninin içerisinde D noktası alınıyor;
s(DAB)=75°, s(DAC)=35°, s(DCA)=30° ve s(DCB)=10° ise, s(ABD) kaç derecedir?
Çözüm:

A A
75° 35° 75° 30°
H
D 30° D 30°
10° T 10°
B CB C
L
1- ACL 40°-40°-100° ikizkenarını oluşturup, [LH]
A yüksekliğini çizelim. LH ve CD doğrularının
kesim noktası T ise s(ATD)=s(DTL)=60° dir.
2- LAT üçgeninde AD ve TD açıortay ise LD açıor-
30°
tay ve dolayısıyla s(LDA)=150° olur.
5° H 3- s(B)+s(D)=30°+150°=180° den ABLD çember-
5° seldir. O halde s(ABD)=s(ALD)=25° dir.

D 60°
60° T 30°
50° 10°
L
102