Page 106 - 100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ-MATEMATİK OLİMPİYATLARI

3. BÖLÜM ÇEMBERLER - I

Soru:
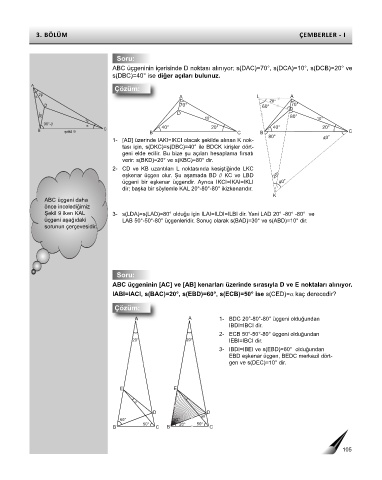
ABC üçgeninin içerisinde D noktası alınıyor; s(DAC)=70°, s(DCA)=10°, s(DCB)=20° ve
s(DBC)=40° ise diğer açıları bulunuz.
A
Çözüm:
2 A L A
20°
D 70° 60° 70°
D
30° D 80°
10° 10°
90°- 40° 20° 40° 20°
B şekil 9 C B C B C
80° 40°
1- [AD] üzerinde IAKI=IKCI olacak şekilde alınan K nok-
tası için, s(DKC)=s(DBC)=40° ile BDCK kirişler dört-
geni elde edilir. Bu bize şu açıları hesaplama fırsatı
verir: s(BKD)=20° ve s(KBC)=80° dir.
2- CD ve KB uzantıları L noktasında kesiştiğinde LKC
eşkenar üçgen olur. Şu aşamada BD // KC ve LBD 20°
üçgeni bir eşkenar üçgendir. Ayrıca IKCI=IKAI=IKLI 40°
dir; başka bir söylemle KAL 20°-80°-80° ikizkenarıdır.
K
ABC üçgeni daha
önce incelediğimiz
Şekil 9 iken KAL 3- s(LDA)=s(LAD)=80° olduğu için ILAI=ILDI=ILBI dir. Yani LAD 20° -80° -80° ve
üçgeni aşağıdaki LAB 50°-50°-80° üçgenleridir. Sonuç olarak s(BAD)=30° ve s(ABD)=10° dir.
sorunun çerçevesidir.

Soru:
ABC üçgeninin [AC] ve [AB] kenarları üzerinde sırasıyla D ve E noktaları alınıyor.
IABI=IACI, s(BAC)=20°, s(EBD)=60°, s(ECB)=50° ise s(CED)=α kaç derecedir?
Çözüm:
A A 1- BDC 20°-80°-80° üçgeni olduğundan
IBDI=IBCI dir.
2- ECB 50°-50°-80° üçgeni olduğundan
20° 20° IEBI=IBCI dir.
3- IBDI=IBEI ve s(EBD)=60° olduğundan
EBD eşkenar üçgen, BEDC merkezil dört-
gen ve s(DEC)=10° dir.

E E

D D
80°
60° 60°
50° 20° 50°
B C B C

105