Page 105 - 100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ-MATEMATİK OLİMPİYATLARI

100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ

Soru ( 1994 ŞANGHAY ) :
s(ABC)=s(ACB)=40° olan bir ABC üçgeninin içerisinde P ve Q noktaları
s(PAB)=s(QAC)=20°, s(PCB)=s(QCA)=10° olacak şekilde alınıyor.
Buna göre B, P, Q noktalarının doğrusal olduğunu gösteriniz.

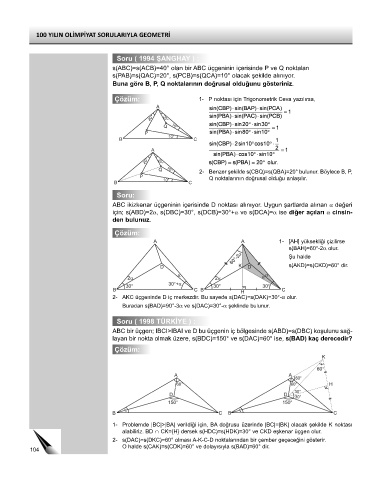
Çözüm: 1- P noktası için Trigonometrik Ceva yazılırsa,
A
20° 20°
Q 10°
P
10°
B C
A
20° 20°
Q 10° 2- Benzer şekilde s(CBQ)=s(QBA)=20° bulunur. Böylece B, P,
P Q noktalarının doğrusal olduğu anlaşılır.
10°
B C
Soru:
ABC ikizkenar üçgeninin içerisinde D noktası alınıyor. Uygun şartlarda alınan α değeri
için; s(ABD)=2α, s(DBC)=30°, s(DCB)=30°+α ve s(DCA)=α ise diğer açıları α cinsin-
den bulunuz.
Çözüm:
1- [AH] yüksekliği çizilirse
s(BAH)=60°-2α olur.
Şu halde
s(AKD)=s(CKD)=60° dir.

2- AKC üçgeninde D iç merkezdir. Bu sayede s(DAC)=s(DAK)=30°-α olur.
Buradan s(BAD)=90°-3α ve s(DAC)=30°-α şeklinde bulunur.
Soru ( 1998 TÜRKİYE ) :
ABC bir üçgen; IBCI>IBAI ve D bu üçgenin iç bölgesinde s(ABD)=s(DBC) koşulunu sağ-
layan bir nokta olmak üzere, s(BDC)=150° ve s(DAC)=60° ise, s(BAD) kaç derecedir?
Çözüm:

1- Problemde |BC|>|BA| verildiği için, BA doğrusu üzerinde |BC|=|BK| olacak şekilde K noktası
alabiliriz. BD ∩ CK={H} dersek s(HDC)=s(HDK)=30° ve CKD eşkenar üçgen olur.
2- s(DAC)=s(DKC)=60° olması A-K-C-D noktalarından bir çember geçeceğini gösterir.
O halde s(CAK)=s(CDK)=60° ve dolayısıyla s(BAD)=60° dir.
104