Page 111 - 100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ-MATEMATİK OLİMPİYATLARI

100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ

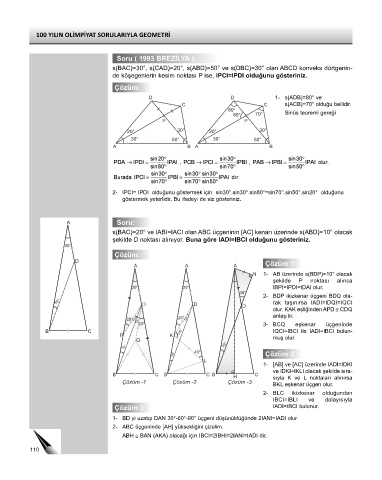
Soru ( 1993 BREZİLYA ):
s(BAC)=30°, s(CAD)=20°, s(ABD)=50° ve s(DBC)=30° olan ABCD konveks dörtgenin-
de köşegenlerin kesim noktası P ise, IPCI=IPDI olduğunu gösteriniz.
Çözüm:
D D 1- s(ADB)=80° ve
C C s(ACB)=70° olduğu bellidir.
80°
80° 70° Sinüs teoremi gereği
P P
20° 30° 20° 30°
30° 50° 30° 50°
A B A B

2- IPCI= IPDI olduğunu göstermek için sin30°.sin30°.sin80°=sin70°.sin50°.sin20° olduğunu
göstermek yeterlidir. Bu ifadeyi de siz gösteriniz.

A Soru:
s(BAC)=20° ve IABI=IACI olan ABC üçgeninin [AC] kenarı üzerinde s(ABD)=10° olacak
şekilde D noktası alınıyor. Buna göre IADI=IBCI olduğunu gösteriniz.
20°
Çözüm:
D Çözüm:1
A A A
N 1- AB üzerinde s(BDP)=10° olacak
şekilde P noktası alınca
20° 20° IBPI=IPDI=IDAI olur.
30°
2- BDP ikizkenar üçgeni BDQ ola-
10° D D rak taşınırsa IADI=IDQI=IQCI
D
olur. KAK eşliğinden APD ≅ CDQ
anlaşılır.
20° 10° 10° 20° 20° 10° 3- BCQ eşkenar üçgeninde
B C 100° IQCI=IBCI ile IADI=IBCI bulun-
P K
Q muş olur.
10° 10°
10° 40° Çözüm:2
L
1- [AB] ve [AC] üzerinde IADI=IDKI
ve IDKI=IKLI olacak şekilde sıra-
B C B C B C
H sıyla K ve L noktaları alınırsa
Çözüm -1 Çözüm -2 Çözüm -3 BKL eşkenar üçgen olur.
2- BLC ikizkenar olduğundan
IBCI=IBLI ve dolayısıyla
Çözüm:3 IADI=IBCI bulunur.
1- BD yi uzatıp DAN 30°-60°-90° üçgeni düşünüldüğünde 2IANI=IADI olur.
2- ABC üçgeninde [AH] yüksekliğini çizelim.
ABH ≅ BAN (AKA) olacağı için IBCI=2IBHI=2IANI=IADI dir.

110