Page 161 - 100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ-MATEMATİK OLİMPİYATLARI

100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ

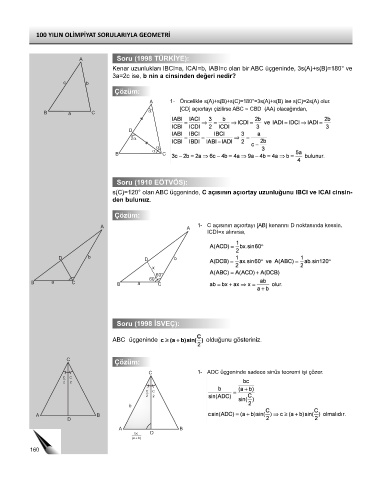
A Soru (1998 TÜRKİYE):
Kenar uzunlukları IBCI=a, ICAI=b, IABI=c olan bir ABC üçgeninde, 3s(A)+s(B)=180° ve
3a=2c ise, b nin a cinsinden değeri nedir?
c b
Çözüm:
A 1- Öncelikle s(A)+s(B)+s(C)=180°=3s(A)+s(B) ise s(C)=2s(A) olur.
[CD] açıortayı çizilirse ABC ≈ CBD (AA) olacağından,
B a C

D
2

B C

Soru (1910 EÖTVÖS):
s(C)=120° olan ABC üçgeninde, C açısının açıortay uzunluğunu IBCI ve ICAI cinsin-
den bulunuz.
Çözüm:

A A 1- C açısının açıortayı [AB] kenarını D noktasında kessin.
ICDI=x alınırsa,

D b D b
x
60°
60°
B a C B a C

Soru (1998 İSVEÇ):

ABC üçgeninde olduğunu gösteriniz.

C
Çözüm:
C 1- ADC üçgeninde sadece sinüs teoremi işi çözer.
C C
2 2
C C
2 2
b
A B
D
A B
bc D
+
(a b)
160