Page 186 - 100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ-MATEMATİK OLİMPİYATLARI

4. BÖLÜM ÜÇGENLER - II

Soru (2005 KANADA):
(a,b,c) pisagor üçlüleri olmak üzere, olduğunu gösteriniz.

Çözüm:
A 1- s(CBA)=β aldığımızda
A
c
b
b c

C a B C a B
2- 0<β<90° olduğundan 0<sin2β≤1 dir. Burada β=45° iken sin2β=1 dir. O halde, sin2β nın en
büyük değeri için (a=b ve β=45° olması halinde); ifadesi minimum değerini alır.

Soru:
C açısı dik olan ABC üçgeninde I ve r sırasıyla içteğet çemberin merkezi ve yarıçapıdır.
AI ve BI doğrularının [BC] ve [AC] kenarlarını kestiği noktalar sırasıyla D ve E ise,

Çözüm:
A A 1- s(A)=2α ve s(B)=2β alırsak s(AIE)=s(DIB)=α+β olur.
Sinüs teoremini kullanalım:

E
+
I E I
r
+
r

C D B C D B

2- s(IEA)=90°+β ve s(IDB)=90°+α ise sin(IEA)=cosβ ve sin(IDB)=cosα dır. Böylece

A
Soru (1996 NORVEÇ):
B' 5
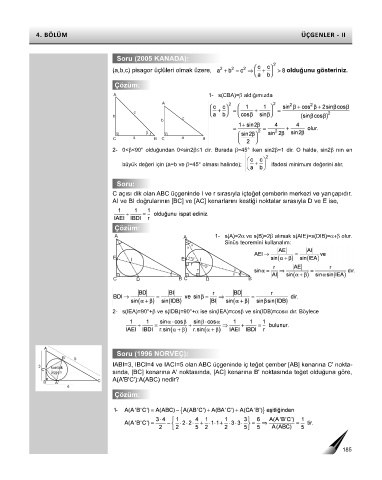
IABI=3, IBCI=4 ve IACI=5 olan ABC üçgeninde iç teğet çember [AB] kenarına C' nokta-
3 kontak
C'
üçgen sında, [BC] kenarına A' noktasında, [AC] kenarına B' noktasında teğet olduğuna göre,
B A' C A(A'B'C'):A(ABC) nedir?
4
Çözüm:

185