Page 19 - 100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ-MATEMATİK OLİMPİYATLARI

100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ

Soru:
AKA bağıntısının KAK bağıntasına denk olduğunu gösteriniz. (AKA→KAK)
Çözüm
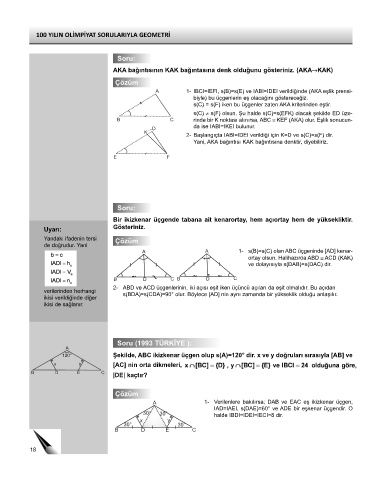
1- IBCI=IEFI, s(B)=s(E) ve IABI=IDEI verildiğinde (AKA eşlik prensi-
biyle) bu üçgenlerin eş olacağını göstereceğiz.
s(C) = s(F) iken bu üçgenler zaten AKA kriterinden eştir.
s(C) ≠ s(F) olsun. Şu halde s(C)=s(EFK) olacak şekilde ED üze-
rinde bir K noktası alınırsa, ABC ≅ KEF (AKA) olur. Eşlik sonucun-
da ise IABI=IKEI bulunur.
2- Başlangıçta IABI=IDEI verildiği için K=D ve s(C)=s(F) dir.
Yani, AKA bağıntısı KAK bağıntısına denktir, diyebiliriz.

Soru:
Bir ikizkenar üçgende tabana ait kenarortay, hem açıortay hem de yüksekliktir.
Uyarı: Gösteriniz.
Yandaki ifadenin tersi Çözüm
de doğrudur. Yani
A A 1- s(B)=s(C) olan ABC üçgeninde [AD] kenar-
ortay olsun. Halihazırda ABD ≅ ACD (KAK)
ve dolayısıyla s(DAB)=s(DAC) dir.

B D C B D C
2- ABD ve ACD üçgenlerinin, iki açısı eşit iken üçüncü açıları da eşit olmalıdır. Bu açıdan
verilerinden herhangi s(BDA)=s(CDA)=90° olur. Böylece [AD] nin aynı zamanda bir yükseklik olduğu anlaşılır.
ikisi verildiğinde diğer
ikisi de sağlanır.

Soru (1993 TÜRKİYE ):
A
120° Şekilde, ABC ikizkenar üçgen olup s(A)=120° dir. x ve y doğruları sırasıyla [AB] ve
x y [AC] nin orta dikmeleri,
B D E C |DE| kaçtır?

Çözüm
A 1- Verilenlere bakılırsa; DAB ve EAC eş ikizkenar üçgen,
IAD=IAEI, s(DAE)=60° ve ADE bir eşkenar üçgendir. O
30° 30° halde IBDI=IDEI=IECI=8 dir.
x y
30° 30°
B D E C

18