Page 200 - 100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ-MATEMATİK OLİMPİYATLARI

4. BÖLÜM ÜÇGENLER - II

Soru:
Bir ABC üçgeninin [BC] ve [AC] kenarları üzerinde [DE] // [AB] olacak şekilde D ve E
noktaları alınıyor. AD ve BE doğruları K noktasında kesişiyor. CK doğrusunun [AB] nin
orta noktasından geçeceğini gösteriniz.

Çözüm:
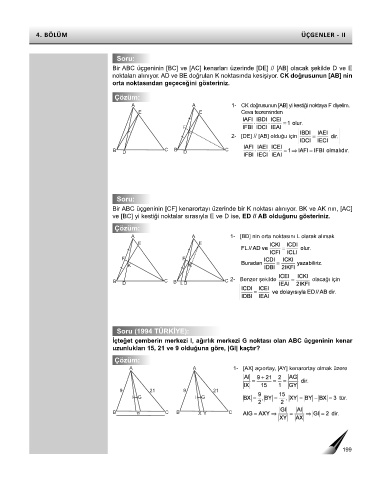
A A 1- CK doğrusunun [AB] yi kestiği noktaya F diyelim.
E E Ceva teoreminden

F
K K
2- [DE] // [AB] olduğu için
B D C B D C

Soru:
Bir ABC üçgeninin [CF] kenarortayı üzerinde bir K noktası alınıyor. BK ve AK nın, [AC]
ve [BC] yi kestiği noktalar sırasıyla E ve D ise, ED // AB olduğunu gösteriniz.
Çözüm:
A A 1- [BD] nin orta noktasını L olarak alırsak
E E
F F
K K
B C B C 2- Benzer şekilde olacağı için
D L D

Soru (1994 TÜRKİYE):
İçteğet çemberin merkezi I, ağırlık merkezi G noktası olan ABC üçgeninin kenar
uzunlukları 15, 21 ve 9 olduğuna göre, |GI| kaçtır?
Çözüm:
A A 1- [AX] açıortay, [AY] kenarortay olmak üzere

9 21 9 21
I G I G
B 15 C B XY C

199