Page 211 - 100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ-MATEMATİK OLİMPİYATLARI

100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ

Soru:
ABC üçgeninde G ağırlık merkezinden geçen, [AB] ve [AC] kenarlarını kesen herhengi
bir d doğrusuna A, B, C noktalarından AA', BB', CC' dikmeleri çiziliyor. Buna göre,
IAA'I=IBB'I+ICC'I olduğunu kanıtlayınız.

Çözüm:
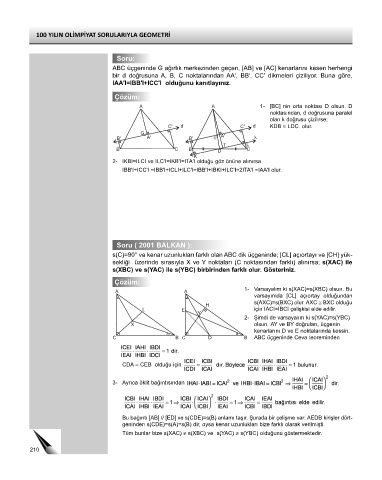
A A 1- [BC] nin orta noktası D olsun. D
noktasından, d doğrusuna paralel
olan k doğrusu çizilirse;
C' d C' d KDB ≅ LDC olur.
G
B' A' B' G A' k
T L
B C B D C
K
2- IKBI=ILCI ve ILC'I=IKB'I=ITA'I olduğu göz önüne alınırsa
IBB'I+ICC'I =IBB'I+ICLI+ILC'I=IBB'I+IBKI+ILC'I=2ITA'I =IAA'I olur.

Soru ( 2001 BALKAN ):
s(C)=90° ve kenar uzunlukları farklı olan ABC dik üçgeninde; [CL] açıortayı ve [CH] yük-
sekliği üzerinde sırasıyla X ve Y noktaları (C noktasından farklı) alınırsa; s(XAC) ile
s(XBC) ve s(YAC) ile s(YBC) birbirinden farklı olur. Gösteriniz.
Çözüm:
1- Varsayalım ki s(XAC)=s(XBC) olsun. Bu
A A
varsayımda [CL] açıortay olduğundan
s(AXC)=s(BXC) olur. AXC ≅ BXC olduğu
H
L E için IACI=IBCI çelişkisi elde edilir.
Y
2- Şimdi de varsayalım ki s(YAC)=s(YBC)
X olsun. AY ve BY doğruları, üçgenin
kenarlarını D ve E noktalarında kessin.
C B C D B ABC üçgeninde Ceva teoreminden

CDA ≈ CEB olduğu için

3- Ayrıca öklit bağıntısından

Bu bağıntı [AB] // [ED] ve s(CDE)=s(B) anlamı taşır. Şurada bir çelişme var: AEDB kirişler dört-
geninden s(CDE)=s(A)=s(B) dir, oysa kenar uzunlukları bize farklı olarak verilmişti.
Tüm bunlar bize s(XAC) ≠ s(XBC) ve s(YAC) ≠ s(YBC) olduğunu göstermektedir.

210