Page 235 - 100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ-MATEMATİK OLİMPİYATLARI

100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ

Soru ( 2004 APMO ):
ABC dar açılı üçgeninin çevrel çemberinin merkezi ve diklik merkezi sırasıyla O ve H ise ;
AOH, BOH ve COH üçgenlerinden birisinin alanının, diğer ikisinin alanları topla-
mına eşit olduğunu gösteriniz.
Çözüm:
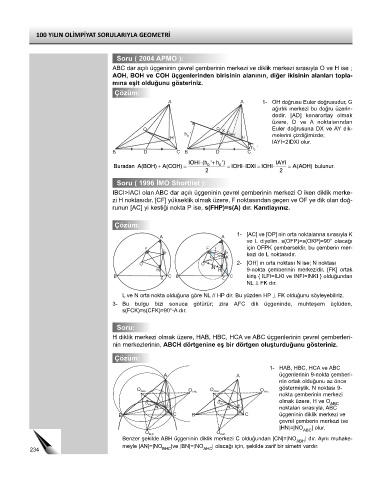
A A 1- OH doğrusu Euler doğrusudur, G
ağırlık merkezi bu doğru üzerin-
dedir. [AD] kenarortay olmak
üzere, D ve A noktalarından
O O X Euler doğrusuna DX ve AY dik-
b h' G Y melerini çizdiğimizde;
H H
IAYI=2IDXI olur.
c h'
B D C B D C

Soru ( 1996 İMO Shortlist ):
IBCI>IACI olan ABC dar açılı üçgeninin çevrel çemberinin merkezi O iken diklik merke-
zi H noktasıdır. [CF] yükseklik olmak üzere, F noktasından geçen ve OF ye dik olan doğ-
runun [AC] yi kestiği nokta P ise, s(FHP)=s(A) dır. Kanıtlayınız.

Çözüm:
1- [AC] ve [OP] nin orta noktalarına sırasıyla K
A A
ve L diyelim. s(OFP)=s(OKP)=90° olacağı
F F için OFPK çemberseldir, bu çemberin mer-
P 90°-A P kezi de L noktasıdır.
L K
O O 2- [OH] ın orta noktası N ise; N noktası
N
H H 90°-A 9-nokta çemberinin merkezidir. [FK] ortak
B C B C kiriş { ILFI=ILKI ve INFI=INKI } olduğundan
Z Z
NL ⊥ FK dır.
L ve N orta nokta olduğuna göre NL // HP dir. Bu yüzden HP ⊥ FK olduğunu söyleyebiliriz.
3- Bu bulgu bizi sonuca götürür; zira AFC dik üçgeninde, muhteşem üçlüden,
s(FCK)=s(CFK)=90°-A dır.
Soru:
H diklik merkezi olmak üzere, HAB, HBC, HCA ve ABC üçgenlerinin çevrel çemberleri-
nin merkezlerinin, ABCH dörtgenine eş bir dörtgen oluşturduğunu gösteriniz.
Çözüm:
1- HAB, HBC, HCA ve ABC
A A üçgenlerinin 9-nokta çemberi-
nin ortak olduğunu az önce
göstermiştik. N noktası 9-
O ABH O ABH
O AHC O AHC
nokta çemberinin merkezi
olmak üzere, H ve O
O ABC ABC
O ABC H
N H N noktaları sırasıyla, ABC
B C B C üçgeninin diklik merkezi ve
çevrel çemberin merkezi ise
|HN|=|NO | olur.
ABC
O BHC O BHC
Benzer şekilde ABH üçgeninin diklik merkezi C olduğundan |CN|=|NO | dır. Aynı muhake-
ABH
meyle |AN|=|NO |ve |BN|=|NO | olacağı için, şekilde zarif bir simetri vardır.
234 BHC AHC