Page 25 - 100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ-MATEMATİK OLİMPİYATLARI

100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ

Soru:
A
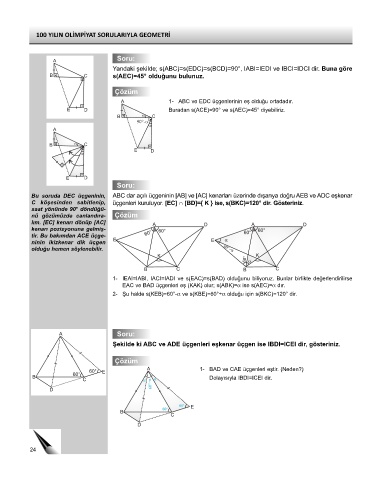
Yandaki şekilde; s(ABC)=s(EDC)=s(BCD)=90°, IABI=IEDI ve IBCI=IDCI dir. Buna göre
B C s(AEC)=45° olduğunu bulunuz.

Çözüm
A 1- ABC ve EDC üçgenlerinin eş olduğu ortadadır.
E D Buradan s(ACE)=90° ve s(AEC)=45° diyebiliriz.
B C
90°-

A
B C
E D

E D
Soru:
Bu soruda DEC üçgeninin, ABC dar açılı üçgeninin [AB] ve [AC] kenarları üzerinde dışarıya doğru AEB ve ADC eşkenar
C köşesinden sabitlenip, üçgenleri kuruluyor. [EC] ∩ [BD]={ K } ise, s(BKC)=120° dir. Gösteriniz.
saat yönünde 90° döndüğü-
nü gözümüzde canlandıra- Çözüm
lım. [EC] kenarı dönüp [AC]
kenarı pozisyonuna gelmiş-
tir. Bu bakımdan ACE üçge-
ninin ikizkenar dik üçgen
olduğu hemen söylenebilir.

1- IEAI=IABI, IACI=IADI ve s(EAC)=s(BAD) olduğunu biliyoruz. Bunlar birlikte değerlendirilirse
EAC ve BAD üçgenleri eş (KAK) olur; s(ABK)=α ise s(AEC)=α dır.
2- Şu halde s(KEB)=60°-α ve s(KBE)=60°+α olduğu için s(BKC)=120° dir.

Soru:
Şekilde ki ABC ve ADE üçgenleri eşkenar üçgen ise IBDI=ICEI dir, gösteriniz.
Çözüm
1- BAD ve CAE üçgenleri eştir. (Neden?)
Dolayısıyla IBDI=ICEI dir.

24