Page 26 - 100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ-MATEMATİK OLİMPİYATLARI

1. BÖLÜM ÜÇGENLER - I

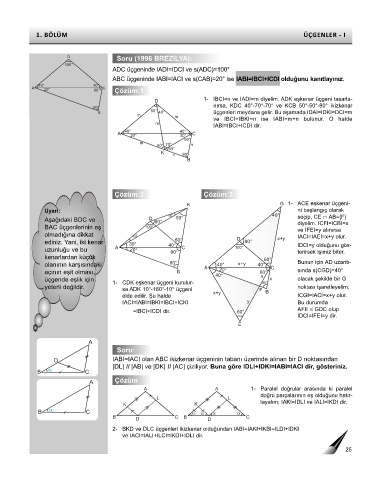
Soru (1996 BREZİLYA):
D
100°
ADC üçgeninde IADI=IDCI ve s(ADC)=100°
ABC üçgeninde IABI=IACI ve s(CAB)=20° ise IABI=IBCI+ICDI olduğunu kanıtlayınız.
40° 40°
A 20° 80° C Çözüm:1
D 1- IBCI=n ve IADI=m diyelim. ADK eşkenar üçgeni tasarla-
nırsa, KDC 40°-70°-70° ve KCB 50°-50°-80° ikizkenar
80°
B 60° 40° üçgenleri meydana gelir. Bu aşamada IDAI=IDKI=DCI=m
m
m
ve IBCI=IBKI=n ise IABI=m+n bulunur. O halde
m
IABI=IBCI+ICDI dir.
40° 40°
A 20° 30° C
50°
m 70°
60° n
50°
K n 80°
B
Çözüm:2 Çözüm:3
K G 1- ACE eşkenar üçgeni-
Uyarı: ni başlangıç olarak
10° 50° 40° seçip, CE ∩ AB={F}
Aşağıdaki BDC ve D 60° diyelim. ICFI=ICBI=x
BAC üçgenlerinin eş 100°
ve IFEI=y alınırsa
olmadığına dikkat 10° x+y IACI=IAEI=x+y olur.
ediniz. Yani, iki kenar 30° 40° 60° D 80° IDCI=y olduğunu gös-
uzunluğu ve bu A 20° C 100°
80° terirsek işimiz biter.
kenarlardan küçük 60°
olanının karşısındaki 80° A 40° x+y 40° C Bunun için AD uzantı-
açının eşit olması, Çözüm -2 B 20° 60° sında s(CGD)=40°
40° x
üçgende eşlik için 1- CDK eşkenar üçgeni kurulur- 80° x olacak şekilde bir G
yeterli değildir. sa ADK 10°-160°-10° üçgeni F B noktası işaretleyelim;
elde edilir. Şu halde x+y ICGI=IACI=x+y olur.
IACI=IABI=IBKI=IBCI+ICKI y Bu durumda
=IBCI+ICDI dir. 60° AFE ≅ GDC olup
Çözüm -3 IDCI=IFEI=y dir.
E

Soru:
IABI=IACI olan ABC ikizkenar üçgeninin tabanı üzerinde alınan bir D noktasından
[DL] II [AB] ve [DK] II [AC] çiziliyor. Buna göre IDLI+IDKI=IABI=IACI dir, gösteriniz.
Çözüm
A A 1- Paralel doğrular arasında ki paralel
doğru parçalarının eş olduğunu hatır-
L L
K K layalım; IAKI=IDLI ve IALI=IKDI dir.

B C B C
D D
2- BKD ve DLC üçgenleri ikizkenar olduğundan IABI=IAKI+IKBI=ILDI+IDKI
ve IACI=IALI+ILCI=IKDI+IDLI dir.

25