Page 278 - 100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ-MATEMATİK OLİMPİYATLARI

ÇOKGENLER - II

Soru:
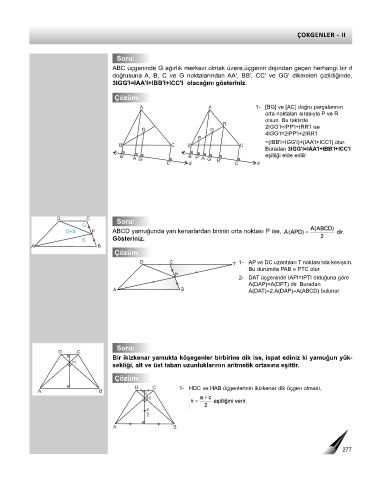
ABC üçgeninde G ağırlık merkezi olmak üzere,üçgenin dışından geçen herhangi bir d
doğrusuna A, B, C ve G noktalarından AA', BB', CC' ve GG' dikmeleri çizildiğinde,
3IGG'I=IAA'I+IBB'I+ICC'I olacağını gösteriniz.

Çözüm:
A A 1- [BG] ve [AC] doğru parçalarının
orta noktaları sırasıyla P ve R
olsun. Bu taktirde
R
G G 2IGG'I=IPP'I+IRR'I ise
4IGG'I=2IPP'I+2IRR'I
P
=(IBB'I+IGG'I)+(IAA'I+ICC'I) olur.
B C B C
Buradan 3IGG'I=IAA'I+IBB'I+ICC'I
B' B' P' eşitliği elde edilir.
A' G' A' G' R'
C' d C' d

D C Soru:
G
G+S P ABCD yamuğunda yan kenarlardan birinin orta noktası P ise,
S Gösteriniz.
A B
Çözüm:
D C T 1- AP ve DC uzantıları T noktasında kesişsin.
Bu durumda PAB ≅ PTC olur.
P
2- DAT üçgeninde IAPI=IPTI olduğuna göre
A(DAP)=A(DPT) dir. Buradan
A B A(DAT)=2.A(DAP)=A(ABCD) bulunur

Soru:
D C
Bir ikizkenar yamukta köşegenler birbirine dik ise, ispat ediniz ki yamuğun yük-
H
sekliği, alt ve üst taban uzunluklarının aritmetik ortasına eşittir.
Çözüm:
D C 1- HDC ve HAB üçgenlerinin ikizkenar dik üçgen olması,
A B c
2
H
a
2
A B

277