Page 279 - 100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ-MATEMATİK OLİMPİYATLARI

100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ

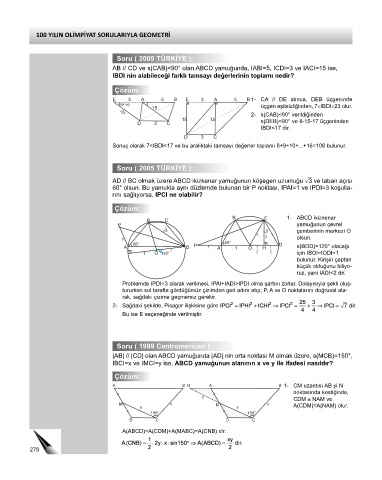
Soru ( 2009 TÜRKİYE ):
AB // CD ve s(CAB)<90° olan ABCD yamuğunda, IABI=5, ICDI=3 ve IACI=15 ise,
IBDI nin alabileceği farklı tamsayı değerlerinin toplamı nedir?

Çözüm:
E 3 A 5 B E 3 A 5 B 1- CA // DE alınca, DEB üçgeninde
dar açı üçgen eşitsizliğinden, 7<IBDI<23 olur.
15
15
2- s(CAB)<90° verildiğinden
15 15
D 3 C s(DEB)<90° ve 8-15-17 üçgeninden
IBDI<17 dir.
D 3 C
Sonuç olarak 7<IBDI<17 ve bu aralıktaki tamsayı değerler toplamı 8+9+10+...+16=108 bulunur.

Soru ( 2005 TÜRKİYE ):
AD // BC olmak üzere ABCD ikizkenar yamuğunun köşegen uzunluğu ñ3 ve taban açısı
60° olsun. Bu yamukla aynı düzlemde bulunan bir P noktası, IPAI=1 ve IPDI=3 koşulla-
rını sağlıyorsa, IPCI ne olabilir?
Çözüm:
B C 1- ABCD ikizkenar
B C
P yamuğunun çevrel
3 3 çemberinin merkezi O
1 2
1 olsun.
60° P 60° D
A D 1 A 1 O 1 H 1 s(BOD)=120° olacağı
1
1 O 120° 2 2 için IBOI=IODI=1
bulunur. Kirişin çaptan
küçük olduğunu biliyo-
ruz, yani IADI<2 dir.
Problemde IPDI=3 olarak verilmesi, IPAI+IADI>IPDI olma şartını zorlar. Dolayısıyla şekli oluş-
tururken sol tarafta gördüğümüz çizimden geri adım atıp; P, A ve D noktalarını doğrusal ala-
rak, sağdaki çizime geçmemiz gerekir.
2- Sağdaki şekilde, Pisagor ilişkisine göre
Bu ise E seçeneğinde verilmiştir.

Soru ( 1999 Centromerican ):
[AB] // [CD] olan ABCD yamuğunda [AD] nin orta noktası M olmak üzere, s(MCB)=150°,
IBCI=x ve IMCI=y ise, ABCD yamuğunun alanının x ve y ile ifadesi nasıldır?
Çözüm:
A B N A B 1- CM uzantısı AB yi N
noktasında kestiğinde,
y
CDM ≅ NAM ve
M x M x A(CDM)=A(NAM) olur.
y y
150° 150°
D C D C
A(ABCD)=A(CDM)+A(MABC)=A(CNB) dir.

278