Page 280 - 100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ-MATEMATİK OLİMPİYATLARI

ÇOKGENLER - II

Soru ( 2001 TÜRKİYE ) :
En büyük kenar uzunluğu 13 ve çevre uzunluğu 28 olan bir ikizkenar yamuğun
alanı en çok kaç olabilir?
Çözüm:
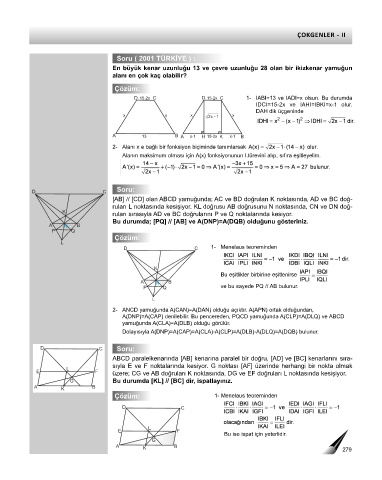
D 15-2x C D 15-2x C 1- IABI=13 ve IADI=x olsun. Bu durumda
IDCI=15-2x ve IAHI=IBKI=x-1 olur.
DAH dik üçgeninde
−
x x x 2x 1 x
A 13 B A x-1 H 15-2x K x-1 B
2- Alanı x e bağlı bir fonksiyon biçiminde tanımlarsak
Alanın maksimum olması için A(x) fonksiyonunun I.türevini alıp, sıfıra eşitleyelim.

Soru:
D C
[AB] // [CD] olan ABCD yamuğunda; AC ve BD doğruları K noktasında, AD ve BC doğ-
ruları L noktasında kesişiyor. KL doğrusu AB doğrusunu N noktasında, CN ve DN doğ-
K
ruları sırasıyla AD ve BC doğrularını P ve Q noktalarında kesiyor.
Bu durumda; [PQ] // [AB] ve A(DNP)=A(DQB) olduğunu gösteriniz.
A N B
P Q
Çözüm:
L
D C 1- Menelaus teoreminden

K
Bu eşitlikler birbirine eşitlenirse
A N B
P Q ve bu sayede PQ // AB bulunur.
L
2- ANCD yamuğunda A(CAN)=A(DAN) olduğu açıktır. A(APN) ortak olduğundan,
A(DNP)=A(CAP) denilebilir. Bu pencereden, PQCD yamuğunda A(CLP)=A(DLQ) ve ABCD
yamuğunda A(CLA)=A(DLB) olduğu görülür.
Dolayısıyla A(DNP)=A(CAP)=A(CLA)-A(CLP)=A(DLB)-A(DLQ)=A(DQB) bulunur.
D C Soru:
ABCD paralelkenarında [AB] kenarına paralel bir doğru, [AD] ve [BC] kenarlarını sıra-
sıyla E ve F noktalarında kesiyor. G noktası [AF] üzerinde herhangi bir nokta olmak
L
E F
üzere; CG ve AB doğruları K noktasında, DG ve EF doğruları L noktasında kesişiyor.
G Bu durumda [KL] // [BC] dir, ispatlayınız.
A K B
Çözüm: 1- Menelaus teoreminden
D C

L
E F
Bu ise ispat için yeterlidir.
G
A B
K 279