Page 285 - 100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ-MATEMATİK OLİMPİYATLARI

100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ

Soru:
E
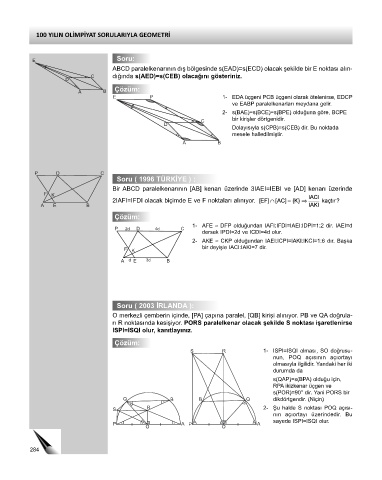
ABCD paralelkenarının dış bölgesinde s(EAD)=s(ECD) olacak şekilde bir E noktası alın-
C dığında s(AED)=s(CEB) olacağını gösteriniz.
D
Çözüm:
A B
E P 1- EDA üçgeni PCB üçgeni olarak ötelenirse, EDCP
ve EABP paralelkenarları meydana gelir.
2- s(BAE)=s(BCE)=s(BPE) olduğuna göre, BCPE
C bir kirişler dörtgenidir.
D
Dolayısıyla s(CPB)=s(CEB) dir. Bu noktada
mesele halledilmiştir.
A B

P D C
Soru ( 1996 TÜRKİYE ) :
Bir ABCD paralelkenarının [AB] kenarı üzerinde 3IAEI=IEBI ve [AD] kenarı üzerinde
F K
2IAFI=IFDI olacak biçimde E ve F noktaları alınıyor.
A E B
Çözüm:
1- AFE ≈ DFP olduğundan IAFI:IFDI=IAEI:IDPI=1:2 dir. IAEI=d
P 2d D 4d C
dersek IPDI=2d ve ICDI=4d olur.
2- AKE ≈ CKP olduğundan IAEI:ICPI=IAKI:IKCI=1:6 dır. Başka
bir deyişle IACI:IAKI=7 dir.
F K
A d E 3d B

Soru ( 2003 İRLANDA ):
O merkezli çemberin içinde, [PA] çapına paralel, [QB] kirişi alınıyor. PB ve QA doğrula-
rı R noktasında kesişiyor. PORS paralelkenar olacak şekilde S noktası işaretlenirse
ISPI=ISQI olur, kanıtlayınız.
Çözüm:
S R 1- ISPI=ISQI olması, SO doğrusu-
nun, POQ açısının açıortayı
olmasıyla ilgilidir. Yandaki her iki
durumda da
s(QAP)=s(BPA) olduğu için,
RPA ikizkenar üçgen ve
s(POR)=90° dir. Yani PORS bir
Q B B Q dikdörtgendir. (Niçin)
R 2- Şu halde S noktası POQ açısı-
S
nın açıortayı üzerindedir. Bu
sayede ISPI=ISQI olur.
P A P A
O O

284