Page 293 - 100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ-MATEMATİK OLİMPİYATLARI

100 YILIN OLİMPİYAT SORULARIYLA GEOMETRİ

Soru ( 1991 AİME ):
ABCD dikdörtgeninde IABI=4 ve IBCI=3 olmak üzere, [AB] kenarı P , P , P ..... P
1 2 3 167
noktalarıyla 168 eşit parçaya bölünüyor. Benzer şekilde [BC] kenarı da Q , Q , Q
167 166 165
.....Q noktalarıyla 168 eşit parçaya bölünerek [P Q ], [P Q ], [P Q ], ..... [P Q ] para-
1 1 1 2 2 3 3 167 167
lelleri çiziliyor. [AD] ve [DC] kenarlarından da aynı tarzla [AC] köşegenine varılıyor.
Böyle elde edilen 335 doğru parçasının uzunlukları toplamını bulunuz.
Çözüm:
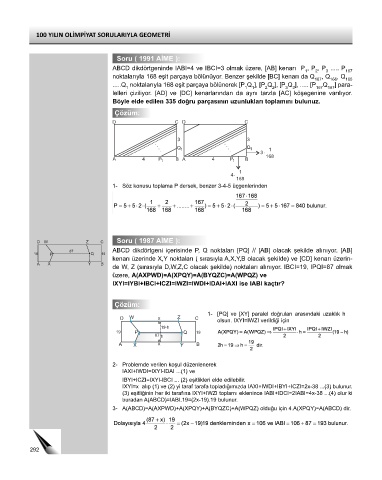
D C D C

3 3
Q 1 Q 1 1
3 ⋅
168
A 4 1 P B A 4 1 P B
4 ⋅ 1
168
1- Söz konusu toplama P dersek, benzer 3-4-5 üçgenlerinden

Soru ( 1987 AİME ):
D W Z C
87 ABCD dikdörtgeni içerisinde P, Q noktaları [PQ] // [AB] olacak şekilde alınıyor. [AB]
19 P Q 19
kenarı üzerinde X,Y noktaları ( sırasıyla A,X,Y,B olacak şekilde) ve [CD] kenarı üzerin-
A X Y B
de W, Z (sırasıyla D,W,Z,C olacak şekilde) noktaları alınıyor. IBCI=19, IPQI=87 olmak
üzere, A(AXPWD)=A(XPQY)=A(BYQZC)=A(WPQZ) ve
IXYI=IYBI+IBCI+ICZI=IWZI=IWDI+IDAI+IAXI ise IABI kaçtır?

Çözüm:
1- [PQ] ve [XY] paralel doğruları arasındaki uzaklık h
D W x Z C
olsun. IXYI=IWZI verildiği için
19-h
19 P Q 19
87 h
A X x Y B

2- Problemde verilen koşul düzenlenerek
IAXI+IWDI=IXYI-IDAI ...(1) ve
IBYI+ICZI=IXYI-IBCI ... (2) eşitlikleri elde edilebilir.
IXYI=x alıp (1) ve (2) yi taraf tarafa topladığımızda IAXI+IWDI+IBYI+ICZI=2x-38 ...(3) bulunur.
(3) eşitliğinin her iki tarafına IXYI+IWZI toplamı eklenince IABI+IDCI=2IABI=4x-38 ...(4) olur ki
buradan A(ABCD)=IABI.19=(2x-19).19 bulunur.
3- A(ABCD)=A(AXPWD)+A(XPQY)+A(BYQZC)+A(WPQZ) olduğu için 4.A(XPQY)=A(ABCD) dir.

292